Precursory slip before large earthquakes - signal or noise?

We evaluate a new defense of noisy data used in a 2023 Science paper

Citation: Bradley, K., Hubbard, J., 2024. Precursory slip before large earthquakes - signal or noise? Earthquake Insights, https://doi.org/10.62481/0ff960fa

Earthquake Insights is an ad-free newsletter written by two earthquake scientists. Our posts are written for a general audience, with some advanced science thrown in! To get these posts delivered by email, become a free subscriber. If you would like to support our work here, please also consider a paid subscription.

Bletery and Nocquet (2023, Science) claimed to find a signal in high-rate GPS data prior to large earthquakes around the world that indicated universal precursory slip over a period of hours. We responded to their paper here on our blog (2023a, 2023b), showing that the apparent signals were removed by noise correction, and therefore not tectonic. Recently, Bletery and Nocquet (2024, preprint) responded to our previous posts, arguing that our approach to noise removal could also remove a real tectonic signal, and that therefore their interpretation “remains entirely plausible.”

Here, we examine the new arguments presented in the preprint, and find them to be pretty misleading. We show that only a very small fraction of a fault slip signal would be removed by common-mode noise correction. We also show that various statistical tests in the new preprint address features of the GPS noise, and are not indicators of earthquake-like signals.

Finally, we discuss a recent re-analysis (Hirose et al., 2024) of independent data that shows that tilt meter records did not detect any precursory slip in the hours before the 2011 Tohoku-Oki earthquake mainshock. This is consistent with our view that a ~M6.9 precursory slip event, as proposed by Bletery and Nocquet (2023), did not occur.

Thus, we stand by our earlier analyses.

A quick note: This post represents our best reading and analysis of this paper. If we have made any mistakes, please let us know and we will correct them immediately. All of our scientific paper analyses always remain free to read and open to comment.

There is a profound, but still largely unanswered, question about how earthquakes begin: do they usually start suddenly and without warning, or are they often preceded by a period of slow, possibly detectable, slip? This question touches on many aspects of our understanding of faults — their geology, physics, and hazards.

In a paper published in Science in 2023, Quentin Bletery and Jean-Mathieu Nocquet presented observational evidence for a widespread precursory phase of slip before large earthquakes. By stacking up high-rate GPS data collected over the two days leading up to 90 large earthquakes, they found a spike at the end of the time series, which led them to conclude that most large earthquakes probably have a ~2 hour period of slow slip leading up to the actual rupture.

They also found evidence for a previously unknown tremor-like behavior expressed as a sinusoidal signal over the 12 hour period leading up to the Tohoku-Oki M9.2 earthquake, suggesting that in some cases the nucleation process might be even longer in duration, and more complex.

Figure 1: Figs. 2CD and 3B of BN23, showing the interpreted 2-hour precursory signal in a global stack of large earthquakes, and an interpreted tremor-like behavior over the day prior to the Tohoku-Oki earthquake. The top two time series both show the global stack over the 48 hours prior to large earthquakes around the world, with either an exponential or sinusoidal best-fit. The bottom time series shows a stack of data from the Japanese network over the 24 hours prior to the Tohoku-Oki earthquake.

To our knowledge, this was the first paper to claim observational evidence for a universal (or at least very common) slow nucleation phase for large earthquakes. It is hard to overstate the implications of this observation — if it is true. If large earthquakes were commonly preceded by several hours of slow slip in the epicentral region, then routine monitoring using dense GPS arrays or other geodetic measurements might possibly provide practical warning of impending large ruptures. With an hour or two to spare, most of the loss of life and some loss of damage could be avoided. If the sinusoidal slip were real, then this warning might be discoverable even days before the mainshock.

We wrote a detailed analysis (part I and part II) of Bletery and Nocquet (2023) — hereafter we label our posts BH23ab and their original paper BN23 — soon after the paper was published in Science. We deep-dived the methods of the paper, and discovered that the analyzed signals were contaminated by a large amount of spatially correlated GPS noise, which is well known to exist in GPS time series data and is usually treated prior to interpretation of the data. The origin and implications of this noise were not addressed in BN23. We showed that a simple correction to remove this noise also removed all of the earthquake-like signals, indicating that the findings of the study were spurious.

Figure 2: An example of the effect of noise removal one the time series for one earthquake (the February 13, 2021 Mw7.2 Fukushima earthquake, an intra-slab event off the eastern coast of Honshu, Japan) Blue dots: raw data. Orange dots: data after removal of the correlated signal from far-field stations only.

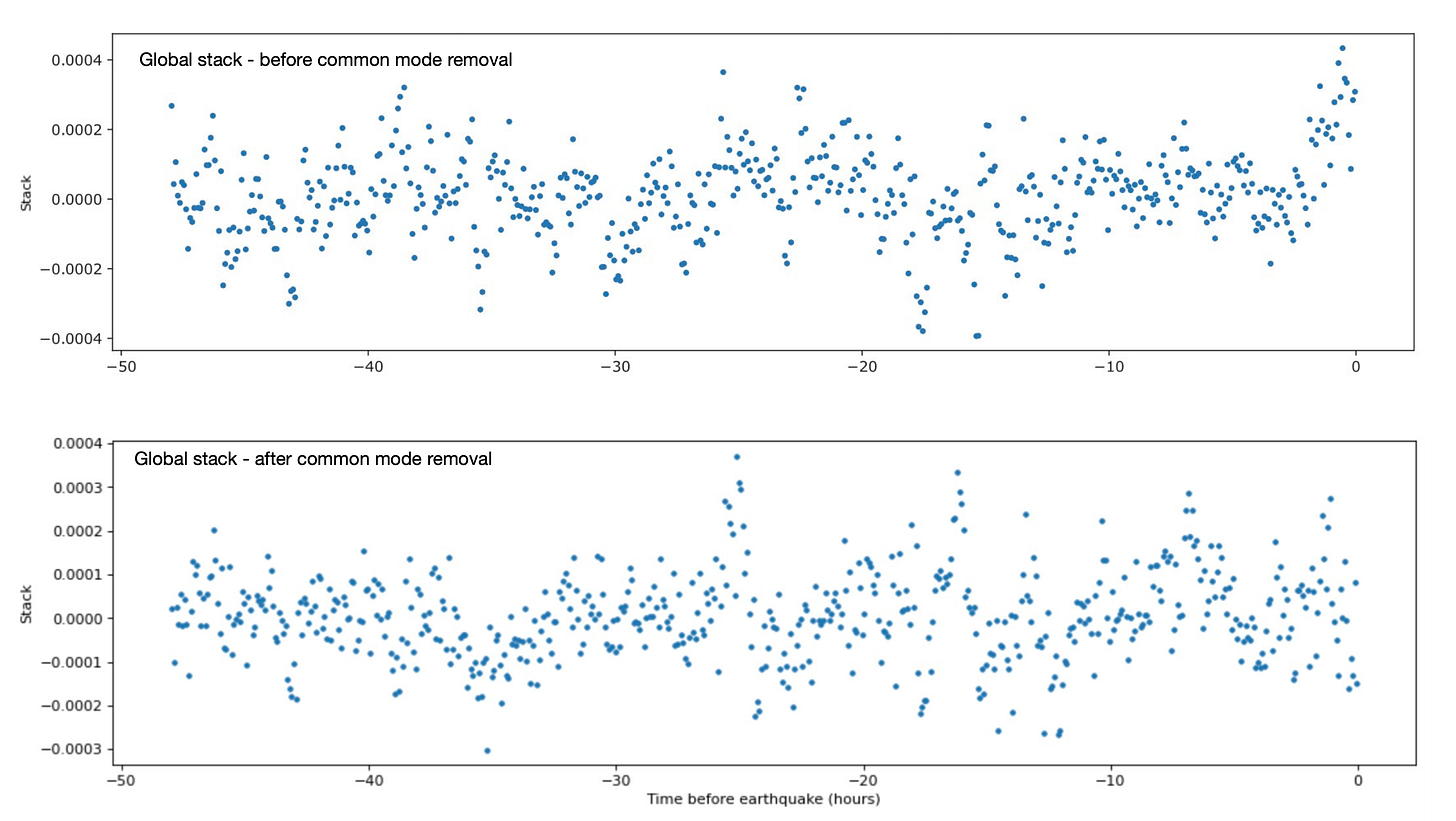
The details are of course available in our previous posts. As a brief refresher, we can just look at Figure 2 above. The blue dots show the raw GPS data for one earthquake, treated according to the method of BN23/24 — this is a time series from the hours before the earthquake, so we do not necessarily expect to see any signal. The orange dots show the same data, after removal of the average motion of GPS sites more than 200km away from the earthquake origin, as proposed in BH23ab. The noise correction collapses the wiggly time series to a much flatter curve. The global stack shown in Figure 1ab represents this type of data, stacked up for many earthquakes.

The effect of this correction on the results of BN23 is tremendous. Once applied, both the final 2-hour spike and the sinusoidal signal before Tohoku-Oki simply disappear.

Figure 3: Global stack before and after common mode removal. Fig. 2A of BN23 and Fig. 9 of BH23a.

After publishing our posts and discussing them with the authors, we submitted a short online comment on the Science website briefly stating our concerns about the data, and linking back to our posts. The authors then responded in the same forum, highlighting some potential ways of showing that earthquake signals might still exist in the data, despite the noise.

Recently, Bletery and Nocquet uploaded a preprint of a complete manuscript that expands on their response on the Science website — hereafter called BN24 — and provides the code supporting their new analysis. They also link to this preprint in a new comment on the Science website. We understand that the preprint is currently submitted to the open access journal Seismica. While that official machine of academia chugs forward, the preprint is publicly available and we will take the opportunity to consider it carefully ourselves.

Figure 4: Header of the new preprint (BN24).

It is important to note that preprints are not final manuscript: they are generally revised before publication based on reviewer and editor comments. However, preprints are also an invitation to public discussion and comment in parallel with, or even before, official peer review.

Before we begin, we would like to commend the authors of BN23/BN24 again for their strong commitment to open science. The original Science paper, the new preprint, and the distributed code and data are examples of the highest attainable standard of open science. (Although the Science paper remains behind a journal paywall, the full text can be read here in a pre-typeset format.) This voluntary sharing of code and data under a Creative Commons license supports the academic push-and-pull that is the only way to ensure that strong results can be confidently cited, and shakier results can be openly debated or disproved. To this end, we also provide the modified code notebooks that support our re-analysis in this post, via this GitHub repository.

Is there convincing evidence that a real precursory earthquake signal exists in the data? Or are we still just looking at well-known but poorly understood GPS noise?

Figure 5: The back-and-forth so far.

---

Agreements

Let’s start by identifying areas of current agreement. Below, we extract some direct quotes from the original paper (BN23), our own posts (BH23ab), and the new preprint (BN24), in order to avoid muddying the waters by paraphrasing. Please note that our own posts are usually written in simplified language for a non-expert audience, so we tend use unprofessional words like “wiggles” instead of “periodic oscillation,” and “hockey stick” instead of “exponential-like signal.” That’s the hard life of science communicators.

Agreement #1: There is an exponential signal in the uncorrected data that disappears when the common mode noise is removed

BN23 found an exponentially growing signal in the last two hours of the global time series stack, which they interpreted as precursory slip of a small fault patch within the nucleation region:

The exponential fit in moment can then be seen as a template of precursory (cumulative) moment release on the fault, suggesting that on average, earthquakes have an exponential-like precursory phase as predicted by laboratory experiments (25–28) and dynamic models (29–31). (BN23)

In BH23ab, we replicated this signal, but noted that it disappeared when we removed the regionally correlated noise:

After removing far-field common mode noise, the hockey stick at the end (time = -2 hours to time = 0 hours) disappears. (BH23a)

BN24 now agree that removal of the average signal of far-field stations (the common mode correction proposed in BH23a) also removes the exponential-like signal.

We verify that, as discussed on informal platforms, (Bradley and Hubbard, 2023a), after such common-mode filtering, the exponential-like signal in Figure 1 and 4.a can no longer be seen (Figure 4.b). (BN24)

Figure 6: Global stack before and after common mode removal. Fig. 2A of BN23 and Fig. 9 of BH23a.

So, we have basic agreement about the presence of correlated GPS noise in the data, and the disappearance of the precursory slip signal upon removal of far-field common mode noise.

Agreement #2: There is a sinusoidal signal in the uncorrected data for the Tohoku-Oki earthquake that disappears with common-mode correction, and which arises from the noise

BN23 interpreted a sinusoidal signal over the 12 hours preceding the Tohoku-Oki M9 earthquake as a tremor-like back and forth slip of a small fault patch in the nucleation area:

It also reveals an unexpected but relatively clear sinusoidal shape, […] strongly suggesting that this sinusoidal behavior is not related to GPS noise but rather is caused by processes taking place in the direct vicinity of the hypocenter of the Tohoku-Oki earthquake. (BN23)

In BH23ab, we proposed that this signal is instead GPS noise, which is often quite periodic:

We believe that these wiggles are inherent to the uncorrected time series at almost all times, for almost all earthquakes, and likely extend to the left of the chart as well. Since the wiggles seem to disappear after noise correction, we suggest that they are not physically related to earthquake nucleation. (BH23a)

BN24 now agree that this signal arises from GPS noise:

Estimating the misfit reduction arising from the periodic oscillation alone, the periodic signal observed before the Tohoku earthquake does not appear to be unique. This invalidates the interpretation we made of this seemingly-oscillatory behavior as a potential precursory signal and rather suggests that the oscillations originate from network-scale correlated noise. (BN24)

Figure 7: Stack for the Tohoku-Oki earthquake before and after common mode removal. Fig. 3A of BN23 and Fig. 11 of BH23a.

Thus, we agree that the periodic signal is part of the GPS noise, is removed by simple noise correction, and is not evidence of an earthquake-related process. This stands in contrast to their interpretation in BN23, and marks a significant back-tracking of the original claims of the paper.

---

Disagreements

So, all of the earthquake-like signals are removed by common-mode noise correction.

“But,” BN24 write,

we show that this common-mode filtering procedure may inadvertently remove an existing tectonic signal. (BN24)

This is the crux of the issue. Is it wrong to remove common-mode noise, as proposed by BH23ab, because of the risk of overcorrecting and obscuring real tectonic signals? Or is noise removal the only way to see through the non-tectonic signal and get at the real motions of the Earth’s surface?

Let’s dig into this issue more deeply.

Noise removal

What is correlated noise? Remember that we are looking at GPS networks — collections of stations over a large area, running continuously. For BN23, the stations produce a location estimate every 5 minutes.

Let’s imagine a few scenarios.

If all stations in a network move exactly the same direction and distance at each time step, then the crust between them neither lengthens nor shortens: there is no actual deformation, just translation. The measured motions, even if very large, have no tectonic meaning. We can correct this correlated noise by removing the average displacement across all stations — called the common mode because it is shared by all stations. In this case, this subtraction would remove all signal and we would be left with a perfectly stationary network.

If all stations were instead affected by a perfectly random motion at each time step, with no net drift, then the average displacement at each time step (the common mode) would be close to zero, and we would not be able to subtract out any motion. We would have to work with the deranged signal we are given (although there would be little information to gain from it).

If we have two superposed signals — a useless but annoyingly large correlated shift of the network, plus a useful but smaller real signal like deformation due to fault slip, then we need to find a way to separate them. Earthquakes shift the nearby crust the most, leaving far-away sites less disturbed, so the signal-to-noise ratio at these stations will be much higher than at stations far from the earthquake source. In contrast, at far-away stations, noise will be a much larger part of the recorded motion. So, we can estimate the correlated network noise by averaging the motion of only the far-field stations. When that average (the common mode) is subtracted from the whole network, we should be left with a much more obviously earthquake-like signal to study.

In BH23ab, we proposed an exclusion distance of 200 km — i.e., we used only data from stations more than 200 km from the proposed signal to calculate the common mode. The plots below show the data before any correction (blue), after removal of the far-field common mode (red), and the common mode itself (black). These data are added up from many earthquakes, with the goal of revealing a subtle but consistent precursory slip signal.

Figure 8: Common-mode correction of the global stack, where the common mode is calculated using stations ≥200km from the earthquake epicenters.

However, BN24 point out that even when near-field stations are excluded, there is a risk of averaging in, and then subtracting out, a real signal, such as the displacement due to an ongoing slow slip event. This is a mathematically true statement, considering that elastic deformations due to earthquakes theoretically affect the whole Earth, at least to a very tiny extent. So, a mean motion calculated from far-field sites will always include at least a little real signal.

The question is: does common mode noise removal actually subtract out too much potential earthquake signal, in the BN23 data? If so, then the spike at the end of the black time series is real data, and our proposed correction is bogus. If not, then that spike is just GPS noise, and the conclusions of BN23 don’t hold up.

How much potential earthquake signal is removed by noise correction? (BN24 suggest that it is too much.)

BN24 argue that the noise removal might be too aggressive, and that we have possibly subtracted out earthquake signals. To support this argument, BN24 present a plot that is intended to show how much earthquake signal might be included in far-field sites.

Here’s the relevant plot (annotated by us).

Figure 9: Fig. 3 of BN24 (annotations added).

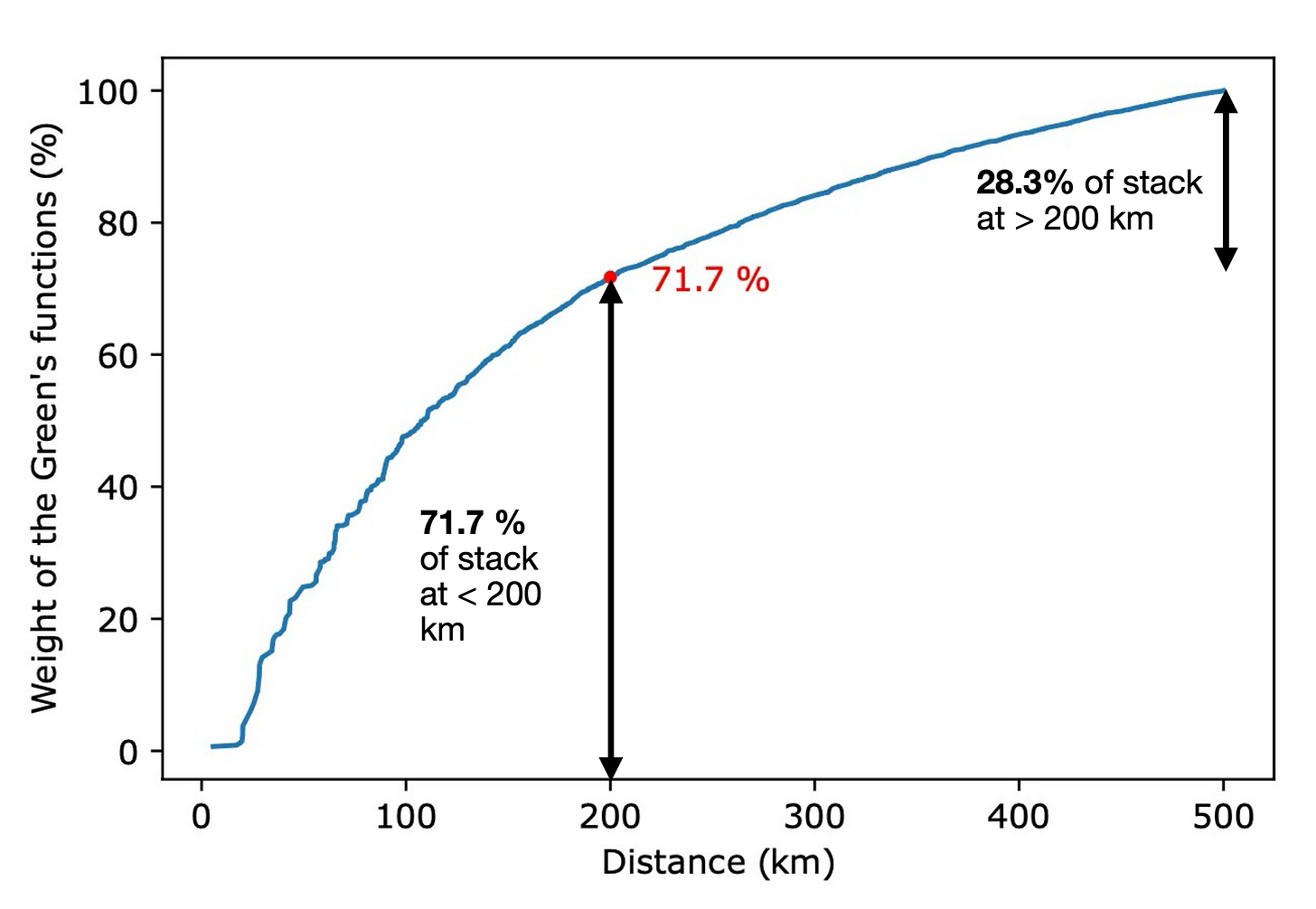
Based on this graph, they write:

we see that observations located more than 200 km away have a cumulative weight on the order of 30% of all observations within a 500 km radius. […] One should not assume that no tectonic signal can be visible in a stack of observations recorded farther than 200 km away from a potential source. (BN24)

Basically, the plot (and text of BN24) says that if we are calculating a mean displacement from stations farther than 200km, we might expect that about about 28.3% of the expected earthquake signal would be contributed by those far-field sites, and therefore that about 28.3% of an earthquake signal would be subtracted out along with the common mode.

Well, that doesn’t sound so bad to us. If we only lose 28% of a tectonic signal from the correction, but reduce the noise level much more, that sounds like a reasonable tradeoff. However, BN24 disagree:

… because the number of observations increases with distance at the same rate than the amplitude of a tectonic signal is expected to decrease, non-negligible tectonic signal contribution in the stack may come from far-field stations (Figure 3). Consequently, the assumption behind the estimation of common-mode noise that far-field stations do not contain tectonic signal may be inaccurate. (BN24)

We are going to address this calculation in more detail in a moment. But first, let’s look at how noise correction affects actual data, as discussed in BN24. That can help get our head out of the clouds a bit.

Testing the effect of noise correction on an imposed earthquake signal

In our view, the most important section of BN24 is a direct test of how noise correction affects potential earthquake signals. While this post will go into much more detail on other topics, this is the truly foundational argument.

BN24 select a time slice of data from the global stack that does not include the proposed precursory slip period. In this time slice, all of the GPS motions should just be actual GPS noise, with no earthquakes present to mess things up. To this real data, they add in an imaginary earthquake signal (a precursory slow-slip event; the orange curve in the figure below). The imaginary signal is calculated by imposing a magnitude 6.4 slow slip event that increases steadily over a 2 hour period — for every considered earthquake. The raw data (not shown) plus the orange curve produce the blue dots.

Figure 10: A 24-hour period of noisy GPS data with a synthetic slow-slip event (the orange curve) added to it. Fig. 6a of BN24.

The spike at the end of the blue time series is pretty clear, which makes sense because it has the orange curve added in:

As expected (since we imposed it), an exponential-like signal appears in the stack before removing the common modes (Figure 6.a). (BN24)

The idea is to now remove the far-field common mode and see what happens — does the imposed earthquake signal disappear? BN24 remove the common mode from all sites located farther than 200 km from each epicenter, as suggested in BH23a, producing the red dots in their panel b:

Figure 11: The same as Figure 8, but with the far-field average subtracted out. Fig. 6b of BN24.

The corrected time series is a lot nicer, with smaller wiggles — a good result from the denoising. The corrected time series also shoots upward at the end, nicely tracking the synthetic signal. To us, the orange line looks almost like a best fit to the red dots, give or take some remaining noise. This indicates to us that the earthquake signal is not affected by the noise removal.

However, BN24 strongly disagree. They specifically do not see an upward swing in the red dots at the end of the time series in panel b:

More surprisingly, the signal can no longer be seen in the stack after removing the common modes (Figure 6.b). (BN24)

We do think the red dots go up at the end, showing that the synthetic earthquake was not removed by subtraction of the common mode. They do not think that the red dots go up at the end, inferring that the synthetic signal was removed.

Finally, let’s look at the common mode noise signal, which was subtracted from the blue dots to get the red dots (black dots in panel c):

Figure 12: The far-field average that was subtracted out from Figure 10 to get Figure 11, i.e. the common mode. Fig. 6c of BN24.

BN24 write:

Even more surprisingly, an exponential-like signal appears in the stack of the common modes alone (Figure 6.c) (BN24)

We agree that the last 2 hours of the black time series looks like they contain an exponential signal — similar to panel b, the dots track the imposed signal — the black time series also has a lot of similar swings earlier on, some even taller. So, this looks to us just like typical noise, with an unfortunate upswing at the end.

Because this is really the most critical part of the argument, we decided to look at this test more carefully. Can we do the same calculation in a way that makes the results unambiguous?

To do this, we made a movie of the same calculation, using the same time window of real data. For each movie frame, we simply shift the imposed earthquake backward in time, repeating the entire calculation for each movie frame. The idea is to make it easier to see whether the earthquake signal (orange curve) re-appears in the red time series (i.e. remains in the analyzable data — which is what BH23ab claim) or shifts into the black time series (i.e. is transferred into the common mode noise — which is what BN24 claim).

From this movie, it is clear that the imposed earthquake signal is almost entirely unaffected by the common mode noise correction. The calculated common mode (bottom panel) only barely changes when a large synthetic earthquake is imposed. (You can see the change if you zoom in on your screen.) The “exponential-like signal” at the end of the common mode time series is present throughout the movie, and is clearly part of the noise. The corrected data (middle panel) clearly shows the earthquake signal.

Remember that this video is for a global stack of the real data used in BN23.

To be quite clear, the results of this specific test are directly cited at the end of BN24 as a reason to suspect the validity of common mode noise removal:

Consistently, we find that when imposing a synthetic signal, the aforementioned common-mode removal procedure inadequately identifies tectonic signal as noise – and noise as signal – (Figure 6), highlighting that there is a definite possibility that a real precursory signal would vanish after removing common modes estimated this way. (BN24)

This conclusion was reached despite the fact that in their discussion, BN24 also write (emphasis ours):

On the other hand, the results of the presented test are highly sensitive to the considered noise. Using different time windows as noise gives different pictures. In the general case, removing translational common modes makes the imposed signal more visible, but the improvement is not systematic. (BN24)

BN24 clearly know that the data shown in their Figure 6 are an exceptional case. We don’t really understand why an exceptional case was presented as the sole example in the preprint, and then used to support their final conclusions.

Why does common mode correction barely affect the earthquake signals?

Far-field common mode noise removal does not remove significant synthetic earthquake signals, and will certainly not cause a real and consistent precursory signal to “vanish.”

The curve from BN24 (Figure 9 above) implied that about 30% of an earthquake signal should be transferred to the far-field common mode. The movie we present indicates that the true loss is far less — more like 5%, if that.

Why is there such a big difference?

It turns out that the curve presented by BN24 is not the correct calculation to make. BH24 calculate what they call the “cumulative amplitude of the Green’s functions.” What does that mean? Well, they impose a set of theoretical earthquakes at each of the locations of the real earthquakes they are studying, and calculate the expected motion at each GPS site. Then they simply add up the lengths of all these motions within a given radius of the earthquakes.

But — that’s not how the stack in BN23 is calculated. The calculation is not just a sum of GPS displacement lengths, but rather a vector dot product. In a vector dot product, you multiply together the lengths of each of two vectors by the cosine of the angle between them. So, if the two vectors are the same, you get the square of the lengths (since cos(0°)=1); if they are perpendicular, you get zero (since cos(90°)=0).

Figure 13: The vector dot product.

In the stacking procedure developed by BN23, each of the GPS vectors is effectively multiplied against the displacement caused by the expected earthquake using the dot product, and then added to the stack. If the GPS field exactly matches the expected earthquake motion, the stack is the sum of squares of the displacements. If the GPS field is zero, the stack is zero.

To get their curve (Figure 9), BN24 simply add up the expected earthquake displacements — but they should instead be (basically) squaring the value at each station: taking the dot-product between the synthetic earthquake displacement field and itself. Since displacements are much larger closer to the epicenter, that means that those nearby stations should be weighted much more heavily than ones that are further away.

Here is what you get if you square the displacements prior to adding them up. Now it is clear that much more of the tectonic signal is contained in the stations close to the epicenter!

Figure 14: A comparison of Fig. 3 of BN24 (yellow, the sum of displacements) with what you get if you square the displacements first to reflect the stacking procedure (blue, the sum of the squares of the displacements).

Now, calculating the impact of common-mode removal isn’t quite that simple, because subtracting out the common mode rotates the vectors a bit, affecting the dot-product a little in a more complicated way. In addition, common-mode removal doesn’t just throw out stations from a given distance away — it calculates their average and subtracts that from the whole vector field. This is all pretty hard to interpret.

Fortunately, we can improve the calculation pretty easily.

Directly calculating the impact of common-mode correction on earthquake signals

Let’s just do the stacking directly, but using the predicted earthquake displacements instead of the actual observed GPS data. For each hypothetical earthquake, we calculate the far-field common mode of the expected displacements, subtract that from the expected displacements, and then stack the resulting vectors as usual (i.e. taking the dot-product with the uncorrected earthquake displacements and adding the result up across all stations).

We define the preservation ratio as the proportion of the original stacked signal that remains after subtracting the far-field mean and re-stacking. This is a direct answer to the question: “how much earthquake signal is left after subtracting the far-field common mode?”

Let’s take the Tohoku-Oki M9.0 earthquake as an example. In the plots below, we tried four different cut-off distances: 2000 km (no noise correction, as no sites are farther than 500 km away), 329 km (using the farthest half of the stations), 200 km (as in BH23ab), and 0 km (all stations are used).

Figure 15: Four examples of a synthetic earthquake at the epicenter of the 2011 Tohoku-Oki M9 event, showing the effect of common-mode correction with different cutoff distances. Red arrows: expected displacements inside the cutoff distance. Blue arrows: expected displacements outside the cutoff distance. Black arrows: remaining displacements after subtraction of the far-field mean vector (common mode).

When we use a very large cutoff distance (e.g. 2000 km), no sites are far-field and so our mean vector is 0. Subtracting this from the original data does nothing, so our corrected stack is the same as the original stack. The preservation ratio is 100%.

When we use more reasonable cutoffs, the preservation ratios for Tohoku-Oki are much higher than the values implied by the graph of BN24 (Figure 14, yellow curve). At 329 km, we get a preservation ratio of 97.3%. At 200 km, we get a preservation ratio of 93%. Even when all of the stations are used to derive the common mode noise (0 km cutoff), we calculate that 81.3% of the stacked signal is still preserved — recall that the BN24 curve shows 0%.

Let’s think about that last result. Why doesn’t subtraction of the mean vector from all sites doesn’t just remove the full signal, as in BN24? Well, the mean vector is an average — somewhere between zero and the maximum earthquake displacement, pointing in some direction that represents the average shift caused by the earthquake. When that vector is subtracted out, the displacements near the epicenter shrink a little bit compared to their large initial lengths. The far-field sites, which had small original motions, may actually move backwards. If you just added up all those corrected displacements you would get zero — but the stacking procedure weights the stations close to the epicenter much more heavily. Those stations still have positive displacements, and end up dominating the signal.

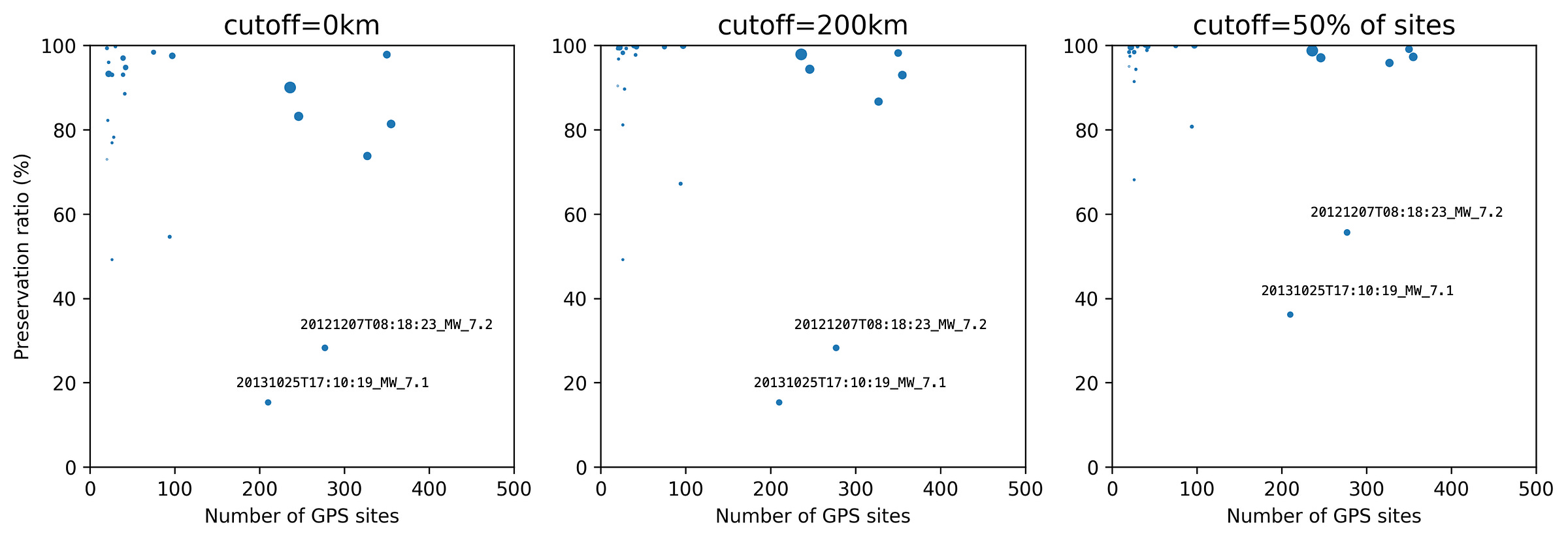
That’s just one example earthquake. What about the rest of them? We calculated the preservation ratios for all earthquakes with N>20 GPS sites, for three cases: d=0km, d=200km, and cutoff=half of sites. In the plots below, the size of each dot is proportional to its contribution to the global stack: the larger the dot, the more weight the earthquake has in the global stack.

Figure 16: Preservation ratios for earthquakes with N>20 sites, for different cutoff distances.

The left plot is the worst case scenario: it subtracts the vector mean of the full earthquake signal. How much of the earthquake signal does it remove? For most earthquakes, the preservation ratio ranges between 70% and 100%, so typically we are losing <30% of the signal.

Two events with more than 200 sites fall below 40%. We were curious about these. It turns out that these two events are located far offshore Japan, with no sites within ~350 km of either earthquake. Because all of the sites are so far away, the gradient in predicted displacement is small for the sites on land, so the mean vector does actually subtract out a lot of the stack. However, because these earthquakes are so distant from the network, they are particularly poor candidates for detecting any kind of subtle earthquake signal.

At d=200 km, we see that nearly all influential earthquakes now have preservation ratios above 80%, and most are above 90%. (The two lowest sites do not change, since they do not have any stations within 200 km.)

When we use the farthest half of sites (right panel), the preservation ratios of the most important events rise above 95%. (For the two earthquakes far offshore Japan, the ratios rise to about 40 and 55%.)

This calculation clearly shows why most earthquake signals should remain nearly untouched by noise correction, with 95%+ of the stacked signal remaining. This explains why the movie above, which shows the impact of common mode correction on an earthquake signal added to real noise, shows such small variations in the common mode time series.

Our take-away: common mode noise removal does not significantly affect earthquake-like signals

This extended analysis shows that common mode noise removal is basically incapable of removing much of a precursory slip signal from stacked data.

If earthquake-like signals really did exist in the raw data, sufficient to stack up to the large spike seen in BN23, we are extremely confident that we would see them in the noise-corrected data as well. There just isn’t a mathematically valid path for earthquake-like signals to be propagated into the common mode noise.

This analysis supports the previous arguments of BH23ab and is sufficient to disqualify all of the conclusions of BN23, because it shows that noise removal really does remove correlated noise, and barely affects earthquake-like signals.

Interlude

If you made it this far but your energy is starting to flag, the next several sections are completely optional. We examine various statistical tests proposed in BN24, in even more gory detail.

So, if you want to dive into some really in-depth technical analysis, read on!

Otherwise, please feel free to skip to the last two sections — the independent test and the final takeaways — without feeling like you missed out on much.

Addressing more tests presented in BN24

BN24 performed several further tests, and in each case they concluded that the tests do indicate the possible or probable existence of earthquake precursors in the data. So, they are worth looking at closely.

However, one very important fact must be kept in mind. BN24 only apply their tests to the uncorrected, noisy data — not the noise-corrected data. So, their tests are querying aspects of the GPS noise. Once the data are corrected for noise, all of the proposed tests fail to have any meaning.

Do the GPS data pinpoint the locations of impending earthquakes?

BN24 suggest that the locations of the impending large earthquakes are predicted by the time series data in the hours leading up to the mainshocks. This is an example of how important it would be if we really could see these earthquakes coming due to the large precursory slip — we could not only say an earthquake was impending, but also where it would nucleate. So, it is particularly important to understand what this test means.

BN24 ask: what if each earthquake had occurred at the same time and with the same slip, but in a different location? Would the last two hours of GPS data still match up with the predicted motion, causing a positive spike at the end of the time series? To answer this question, they move each earthquake around to nearby locations, shifting it west/east/north/south on a regular grid, and then calculate how strong the final ‘uptick’ of the time series is, compared to the previous 46 hours of data.

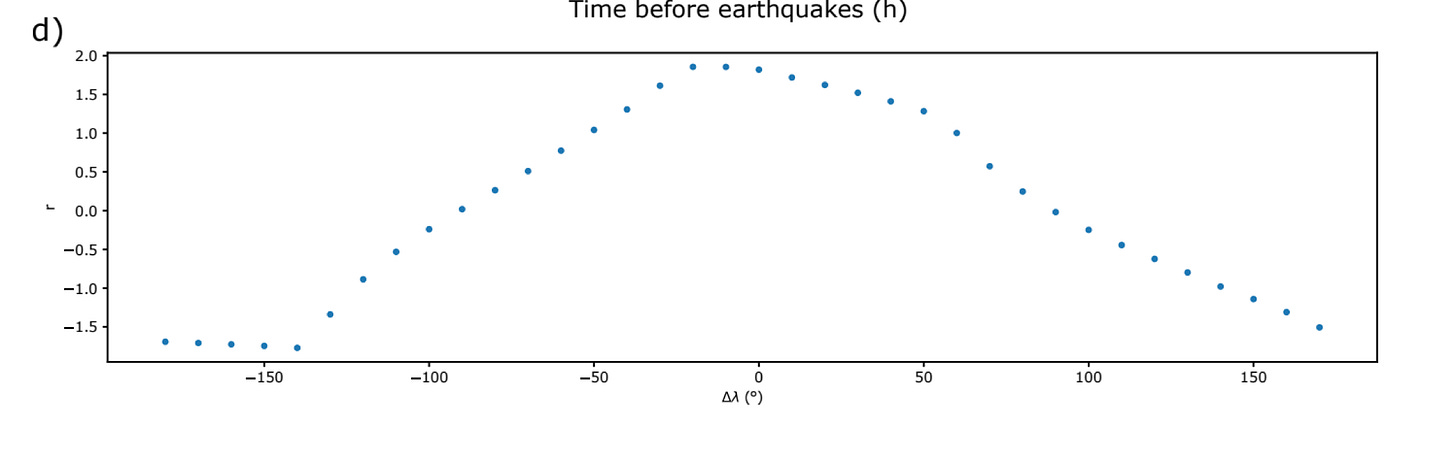
Specifically, they map out the variation in the parameter r, as described in BN23. This parameter measures the height of the final spike (after smoothing the data using a sliding time window) versus the height of the time series before the spike (also using smoothed data). So when r=2, the final spike is twice as tall as the maximum over the previous two days.

Figure 17: The r-value (strength of the final spike) if the earthquake locations are moved en masse to locations east/west/north/south of the true epicentral locations. The red star matches the largest value of r. Fig. 11 of BN24.

The yellow circles show locations where the two-hour spike is particularly large. Blue circles show where it is particularly small, or even negative.

When all earthquakes are stacked together, the true earthquake location (the red star) does in fact coincide with the maximum value of r. The spike is largest where the earthquakes eventually occur.

BN24 state that this should only happen if a precursory signal does in fact exist:

We find that r is maximum at the actual location of the earthquakes (Figure 11), strengthening the idea that the signal originates from precursory slip in the direct vicinity of the hypocenters of the impending earthquakes. (BN24)

…

This test highlights that, though low-amplitude and not robust to common-mode filtering, the signal points to the location of the upcoming earthquakes, an observation difficult to reconcile with the hypothesis that this signal originates from noise. (BN24)

Because the data in this test are stacked up over all of the earthquakes, we find it hard to visualize what is actually happening, and how each earthquake contributes to the result. However, there is a relatively easy way to demonstrate why this test doesn’t actually work.

Let’s revisit a similar test which was published in the supplement of the BN23, which also searched for the spatial location of the observed signals for the case of the Tohoku-Oki earthquake.

BN23 conducted a grid search around the Tohoku-Oki M9.0 epicenter, examining how two different signals change when the earthquake location is moved around:

1. The amplitude of the 12-hour periodic oscillation, and

2. The size of the spike in the final two hours of data.

Because these tests were performed for a single earthquake, we can make maps and explore the data more intuitively than for a global earthquake stack.

For the periodic oscillation signal, BN23 estimated which earthquake location yields the stack with the largest sinusoidal motion over the day prior. The location of the earthquake (red star) closely matched the location that produced the strongest sinusoidal signal in the stacked time series:

Figure 18: Colored circles show how well the data over the 24 hours prior to the Tohoku-Oki earthquake are fit by a sinusoidal curve, testing different locations as the source of the signal. Fig. S11a of BN23.

In BN23, this match was interpreted as resolving the physical process of pre-earthquake tremor-like motion, and was used to support the idea that the periodic signal was a real earthquake process ongoing for many hours before the mainshock.

Similarly, the average value of the data stack during the last two hours (when the hockey stick is going steeply up — (and normalized by the sum of the expected displacements)) also points out the area of the upcoming earthquake, more or less:

Figure 19: Colored circles show how large of a final spike is produced when different locations are used as the source of the signal. Fig. S11b of BN23.

Because the final spike is tallest when the grid location nearly matches the origin location (the maximum is actually offset to the west by one grid cell, 50km), it also seems like there is an earthquake-related signal in the data before the earthquake happens.

But does this “pointing out” of the epicenter happen only in the last 2 hours of data, when the fault might actually be slipping? If so, it may in fact be a subtle earthquake signal.

Or, does this “pointing out” also happen during other, non-precursory times? If so, it clearly cannot be interpreted as an earthquake-related signal.

To test this, we recalculated Figure 19 for each 1-hour time window over the 24 hours before the earthquake. For each time window, we asked whether the maximum calculated value coincided with the earthquake location, or at any cell adjacent to the earthquake location (as with the result of BN23). Recall that no tectonic signal is proposed, except in the last two hours.

What are the results? The following figure summarizes. Don’t worry about the tiny maps at top — we will show some example panels in a moment. The green checkmarks and green shaded windows on the time series indicate when the signal does ‘point out’ the earthquake location. The red X’s and unshaded windows indicate when it does not.

Figure 20: Calculating the location that produces the strongest spike for each 1-hour time window over the day prior to the Tohoku-Oki earthquake. Time windows shown in green match to grid locations either at or next to the true epicenter.

About 40% of the time over the day prior to the earthquake, the calculated upward spike is tallest near the epicenter location. In general, this happens when the stack is positive. When the time series goes negative, the epicenter is definitely not preferred.

Here are some actually visible panels of the hourly calculations. Two show preferred locations near the epicenter, two show them far from the epicenter.

Figure 21: Like Figure 19, but for different time windows when no earthquake slip is inferred.

This demonstrates that the “pointing out” of the earthquake location by the data in the final two hours is not unique to the time of proposed precursory slip — and is therefore not an indicator of an earthquake precursor signal in the data. Instead, it is a common feature of the time series and arises from the common mode noise.

How can we explain this counter-intuitive result?

We believe that the effect arises from a unique combination of factors, which certainly exists for Japan and might also be present in some way for the other regional networks. First, the earthquake epicenter is near the middle latitude of the GPS network, and is located on its eastern side. Second, the slip of the earthquake is directed almost due east. Third, the correlated noise in the network includes a significant east-west component — i.e., the noisy “jiggle” is not randomly oriented, but often side-to-side.

When these factors combine, the GPS noise alone will tend to point out the epicenter and slip direction of the Tohoku-Oki earthquake — even though it is completely unrelated. If all of the stations appear to be moving east, then the best-fit “earthquake” must be in the middle latitudes, with about half the stations to the north and half to the south. The “earthquake” also has to be offshore, so that all of the synthetic slip is eastward, but not so far offshore that the stacked signal is too small.

This also explains why the full 24-hour sinusoidal signal (now acknowledged by BN24 to arise from the GPS noise) also seemed to arise from the epicentral area — it is not a feature of repeated fault-slip-and-backslip over the day prior to the earthquake, as interpreted by BN23. It is just the unfortunate nature of the common mode noise, the network geometry, and the slip direction of megathrust earthquakes in this area. The fact that the sinusoidal noise highlights the Tohoku-Oki earthquake location is actually a strong argument against use of these kinds of spatial tests!

Let’s return to the result in BN24 with this new understanding.

To test whether this apparent location signal arises mainly from the Japanese network configuration and the several megathrust earthquakes in that area like the Tohoku-Oki earthquake, we recalculated the figure of BN24. We excluded the four thrust events located offshore of east Honshu, which should all be affected by this specific combination of factors. (One earthquake occurred in 2005; the other three are related to the 2011 sequence.)

Figure 22: Like Figure 17, but excluding the four thrust earthquakes offshore east Honshu.

After removing those events, the earthquake epicenter is no longer the preferred location for the remaining global stack. This suggests that the Japanese GPS network really does dominate the apparent alignment of the epicenter with the positive spikes, in the global stack.

Thus, we disagree with BN24 about the implications of these spatial tests. They are not an indicator of an earthquake precursor signal, in Japan or elsewhere.

Do the GPS data predict the slip direction of impending earthquakes?

A similar test presented in BN24 assesses whether the slip directions of the impending earthquakes are embedded in the pre-earthquake time series signal. This test is analogous to the previous test, but instead of varying the earthquake location, only the earthquake slip direction is changed, by rotating the rake angle λ for all earthquakes, simultaneously. This rotation affects the expected ground motions, changing the resulting data stack.

The rationale behind this test is that if the new data stacks (after rotation of the rake) don’t show the precursory slip in the hours before the earthquake, it must be because a real earthquake signal in the data is being misfit by the wrong earthquake slip direction.

And that is the conclusion of BN24:

Perturbing the rake angle λ by large values (∆λ ∈ [−180◦, −90◦, 90◦]) the signal completely vanishes (Figure 12.a-c). We generalize the test by calculating r for rake perturbation increments of 10° from −180° to 170°. We find that r is large (r ≥ 1.5) only for small perturbations of the rake angle (|∆λ| ≤ 30°) — and r < 1.5 for|∆λ| > 30° —, further suggesting that the signal is related to the upcoming earthquakes. (BN24)

Figure 23: The r value calculated when the slip directions of the earthquakes are uniformly rotated by ∆λ. There is a peak near 0° and the negative values near ±180°. Fig. 12d of BN24.

Let’s think about this. What is this test actually doing?

An important mathematical fact about elastic deformations is that when we rotate the rake angle around completely — by ∆λ=180° or ∆λ=-180°, the expected motions are precisely backward from the ‘real’ ones, with the same amplitude. We actually recover the original time series, but flipped upside down! This panel from BN24 shows the perfectly flipped signal:

Figure 24: The global stack, when the slip directions are rotated by 180°. Fig. 12a of BN24.

Because we started with a time series that has a tall spike at the end (r is large), at ∆λ=-180° we have a series with a negative spike (r is negative).

In between the original and -180/180° rotation, the expected displacements at each site change smoothly but not symmetrically. At ∆λ=+90°, some of the expected motions might be orthogonal to the original ones, or they could be almost parallel to them — it depends on the pattern for each earthquake.

However, it will always be true that the time series for a rake of ∆λ=+90° is identical to that of the ∆λ=-90°, but flipped upside down, as shown in these panels from BN24.

Figure 25: The global stack, when the slip directions are rotated by -90° (top) or +90° (bottom). Fig. 12bc of BN24.

This doesn’t mean that the resulting distribution of r will by symmetrical around ∆λ=0°. That is because r compares the final point in the smoothed curve to its maximum over the previous 2 days (minus the last 2 hours). When the curve is flipped over, we are effectively using the minimum instead.

Notice how for ∆λ=-90°/+90°, the terminal spike has disappeared. BN24 interpret this as proof that the slip direction of the impending earthquake is somehow embedded in the time series, at least for the last 2 hours.

However, we have to remember where we are starting from. The BN23 paper was published because it saw a large positive spike in the last 2 hours, larger than any other spike in the previous 48 hours. This means that, on average, the GPS motions were more aligned with the earthquake slip direction at that time than at any other earlier time.

Because the positive spike must become negative at ∆λ=-180°/+180° rotation, there will always be a hump in the middle of the r-vs-λ curve, for the BN23 data. That is a simple reflection of how r — the parameter measuring the last 2-hour spike — is defined.

We knew going in that the r value would be high for λ close to 0°, and we should have known that it would have large negative values for λ close to 180° — simply based on the shape of the original spike. The r value has to cycle from one to the other, going through 0° in between.

So, it is unsurprising to see that the high r values are (as BN24 describes them) “large (r ≥ 1.5) only for small perturbations of the rake angle (|∆λ| ≤ 30°)”. Such an outcome could reasonably have been expected from the shape of the original spike, and does not provide much new information.

In the end, this test simply doesn’t say much, besides showing off a fundamental mathematical property: the stacked data flip upside down when the earthquake slip directions rotate by 180°!

Statistical uniqueness arguments

Simply looking at the global stack, the spike in the two hours before each earthquake does seem to stick out as unusual. BN23 and BN24 argue that this signal is so unusual that it must have an origin as an earthquake process, and not noise.

BN23 and BN24 evaluate the uniqueness of the 2-hour precursory spike by various methods, like randomly resampling the GPS time series for each station over different time windows, or shuffling the data in a fairly technical way, and calculating how often they see a last-2-hour spike that is similarly tall and steep. In BN23, the definition of this spike is quite specific:

• n (number of monotonically increasing samples in the 1 hour 50 minute windowed time series) >= 23, and

• r (the ratio of the last point in the windowed time series to the peak in the prior 48 hours, excluding the last 2 hours) >= 1.82.

With 100,000 samples, the signal only simultaneously exceeds these values of n and r in the last two hours about 0.03% of the time.

These two tests consistently indicate that network-scale correlated noise may coincidentally sum up constructively to produce an exponential-like signal similar to what we observe but the likelihood of such a thing to happen precisely at the time we observe it is on the order of 0.03%. We emphasize that these two tests provide statistics that take into account the uneven relative weight of the different events and network-scale correlated noise, overall indicating very low likelihood that the signal randomly arises from (common-mode) noise. (BN23)

Once again, this has proved to be a particularly tricky test to wrap our heads around.

One thing that stood out to us was that the values of n and r used in this uniqueness calculation depend on the chosen averaging window width. Why did BN23 choose 1 hour and 50 minutes as the relevant window, and why is n=23 significant?

We explored this question by calculating the values of n and r for the BN23 data, using a range of window widths. The chosen window width (1 hour and 50 minutes) clearly optimizes both parameters (n and r). Making the window narrower or wider results in tradeoffs of one or the other parameter. The figures below show how r and n vary with different window widths (expressed as the number of 5 minute samples, 22 samples = 110 minutes = 1 hour and 50 minutes). The 1 hour and 50 minute window is highlighted as an orange star.

Figure 26: How r and n vary depending on the window width (where each sample = 5 minutes). The orange stars mark 22 samples = 1 hour and 50 minutes.

Note how when you shorten the window width to 20 samples (1 hour and 40 minutes), n drops to a very low value. That is because, at that window width, the last observation is a drop from the previous one. Also note how for wider windows, r steadily decreases. This is because the wider smoothing window integrates more of the earlier, lower data points, drawing r downward.

BN23 proposed that a window width of 1 hour 50 minutes is special, capturing a unique geological signal — so unique that the relevant r (≥1.82) and n (≥23) only show up simultaneously 0.03% of the time in the noise. (BN24 clarify that r≥1.82 occurs 0.2% of the time, and n≥23 occurs 0.9% of the time; when both statistical measures are combined, the two metrics are achieved simultaneously only 0.02% of the time.)

If this statistical measure of ‘earthquakiness’ is a valid way to characterize the BN23 data, and is not just the most conveniently suggestive time window, then it should presumably still work when newer earthquakes are added to the stack.

BN24 present an updated global stack that includes 20 newer earthquakes, including several large, well-monitored events that contribute a lot to the stack. Here are the time series of the four added events that have significant weight in the stack. The raw data are in blue, and the noise corrected data removing the far field average (cutoff=200km) are orange:

Figure 27: Stacks for four recent earthquakes considered in BN24; blue = uncorrected data, orange = data with common mode noise removed, with a cutoff distance of 200 km.

You can see that two of the events (2024-01-01; the Noto, Japan earthquake, and 2021-03-20) have sort-of-spikes during the last several hours, in the raw data. However, the spikes both drop back to near zero before the series end. As with previous earthquakes, common mode noise removal collapses the wiggliness of these time series and suppresses the final spikes, showing that network-correlated noise contributes most of any precursor-like signal for each event.

So, what happens when these earthquakes are added in to the global stack? Let’s compare the BN23 and BN24 stacks, along with some moving averages for different time window lengths.

Figure 28: Global stacks for the BN23 (left) and updated BN24 (right) earthquakes. Middle row shows moving averages with time window of 1 hour and 50 minutes, proposed by BN23. Bottom row shows moving averages with time window of 3 hours, newly proposed by BN24.

The raw time series of BN24 (top right) now turns downward at the end, because the newly added earthquakes drop in the last few data points. The fall is quite consistent, and it has an effect on the moving average with a 1 hour 50 minute window (middle right), which now also turns over at the end, yielding n of 0 or 1. The signal therefore must become ~100x less statistically unique, by the BN23 criteria, since n is no longer special.

To avoid this terminal fall — and reduction in uniqueness — BN24 newly propose use of a longer 3-hour window (Figure 28 bottom right). However, when the BN23 data (Figure 28 bottom left) are recalculated using this 3-hour window, both r and n suddenly look a lot less impressive.

BN24 suggest abandoning the metric of n all together, relying only on r.

Even though the exponential-like trend is arguably not as visually impressive as in Figure 1 because of a high-frequency negative trend in the minutes preceding the events, the positive trend in the previously identified time window (1 h 50 min) is actually strengthened by the addition of the recent events (r = 2.1). (BN24)

In other words, it is clear that there was nothing special about the original chosen window of 1 hour 50 minutes — and therefore no reason to choose it, except for the fact that it provided the most compelling statistics. Similarly, there is nothing special about a window of 3 hours. Furthermore, there is nothing special about monotonic increases, since this metric can easily be upset by what BN24 describe as “high-frequency fluctuations.” The high-frequency fluctuations — which seem to hide the necessarily increasing precursory slip — are in fact easily removable common mode noise.

What can we take away from this analysis? BN23 chose specific metrics that emphasize the uniqueness of the signal; failing to meet that standard, BN24 shift the goalposts to emphasize an alternate metric of uniqueness.

In any case, even if there is something highly unusual about the stacked GPS signal in the hours before big earthquakes, it is important to remember that it has more to do with correlated GPS noise than with earthquake behavior — because the final spike, after all, disappears when the far-field noise is removed.

Some thoughts on the unusual two-hour ‘precursory’ spike

Ultimately, we agree that the height of the final spike in the uncorrected global stack seems unusually tall, at least in the data we have looked at. That is, of course, why BN23 was published in Science — the raw signal simply looks like it is significant.

The relevant question is: why does the far-field GPS noise seem unusual in the hours before the mainshock?

One option is that final spike just random chance — it’s just the unfortunate alignment of the periodic GPS noise from several of the most influential events (those with stations located closest to the earthquake, which contribute a lot to the global stack). We think there is a simple way to show how tenuous the 2-hour spike really is.

Using the extended BN24 dataset, we ordered the earthquakes by the amplitude of their raw signal over the 48-24 hour period before the mainshock. Events at the top of this list had large signals more than 24 hours before the earthquake — a sign that GPS noise contributes a lot to those specific time series. Since this noise metric does not include the last day of data, there is no a priori reason to believe that it is related to the amplitude of the final spike — if the spike is related to a real earthquake signal rather than noise.

When we exclude only the top three events, the final spike simply disappears from the global stack, even without any noise correction (107 earthquakes remain in this global stack). The blue dots show the full dataset, the red dots exclude the top three earthquakes.

Figure 29: The global stack with the full BN24 dataset (blue dots), and with the top three noisiest events excluded, as described in the text (red). See Figure 31 for the list of excluded earthquakes.

Interestingly, common mode noise correction (cutoff=200 km) doesn’t have much effect on the global stack once we have excluded these few events. In the figure below, we have also excluded events with very few GPS sites, to allow calculation of the noise-correction — they make very little difference to the stack. The green series at top is the global stack (minus the big three earthquakes), and the blue series is the noise-corrected data. Neither series shows a final spike.

Figure 30: Global stack excluding the three noisiest earthquakes. Top (green): no noise correction. Bottom (blue): with common mode noise removed.

In fact, for the original BN23 data, we only have to exclude one earthquake: the 2010 El Mayor-Cucapah earthquake, to remove the final spike! (This earthquake is also one of the “top three” in the updated BN24 dataset.)

Why are these top three earthquakes so influential? Each one has a few very large expected displacements due to the close proximity to the earthquake epicenter. These nearby sites dominate the stack, amplifying the signal — and the noise — from that network into the global stack. They also represent only two regional GPS networks: in the USA and Japan.

Figure 31: Synthetic earthquake displacements used in the dot product to generate the stack for each of the three noisiest earthquakes in the BN24 dataset.

So, while there are 110 earthquakes included in BN24, and 90 in BN23, only a few of them actually contribute much to the final spike. The probability of finding a final spike in the global stack is just the chance that these few big earthquakes have final upward swings of their overall noisy and semi-periodic signals.

So, we think that this is probably just an unlucky situation where the periodic noise in a few different GPS networks happens to line up better in the hours before the earthquakes, than over the two days prior.

However, there are some other ideas to consider.

An astute reader of ours commented that the coseismic signal from the subsequent earthquake might be smoothed backward in time by the GPS processing, contaminating the time series before the earthquake with an earthquake-like signal.

BN24 looked into this and consulted directly with the GPS data provider at UNR. They concluded that some smoothing of signal backwards in time may occur, but it is really hard to understand how, and to what degree, this happens, because of the complex modeling required to turn the raw GPS signal into useful time series displacements. This highlights the tremendous difficulty of understanding high-rate GPS noise. The enormous chain of calculations and corrections embedded into each data point makes it extremely hard to keep track of how each step or assumption affects the resulting data.

Like BN24, we think that we can exclude the possibility that a small fraction of the actual coseismic offset was back-propagated in time on a per-station basis. Our argument is different than BN24’s: we believe that such a signal would look similar enough to a real earthquake signal, that it would not be subtracted during noise correction.

Ok, we think we have done enough work to understand the main arguments of BN24. Can we find any external information that might shed light on this issue?

---

An independent test: tilt meter records indicate no large precursory slip prior to the Tohoku-Oki earthquake

In BH23ab, we observed a long-term rising trend in the de-noised data before the 2011 M9 Tohoku-Oki earthquake, and asked whether this could be a real observation of the ongoing tectonic activity that began with the M7.2 foreshock two days earlier. We now have an updated observation-based paper with which to compare.

A new open-access paper has just been published in GRL, which tackles the idea of a precursory slip phase in the hours before the Tohoku-Oki earthquake.

Figure 32: Header of Hirose et al. (2024).

Following up on a paper published soon after the earthquake in 2011 (and not cited by BN23 or BN24), and stimulated by our discussions in BH23ab, Hirose et al. (2024) re-examine precise measurements of the tilt of Earth’s surface, also from sites distributed across Japan. Because fault slip necessarily deforms the surrounding crust, causing Earth’s surface to tilt in different directions, these kinds of measurements can directly record deformation from earthquakes or from slow-slip events. They are also entirely independent measurements from GPS, and do not suffer from the uncertainties that result in correlated GPS noise.

To create a time series comparable to the results of BN23, Hirose et al. adopted the exact same data stacking approach, generating directly comparable time series.

What did they find?

The stacked tilt meter data clearly resolve many aspects of the foreshock sequence. Starting on March 9, there is a sudden and widespread tilting of the land surface in Japan. This signal indicates that the tilt meter network is sensitive enough to pick up large earthquake behavior happening in the epicentral area offshore.

In the figure below, we have added annotations to the original curves from the paper:

Figure 33: Tilt meter data from Tohoku-Oki, stacked according to the method of BN23. Figs. 3bd of Hirose et al. (2024), rearranged and annotated.

That tilting seems to visually match the curve in the noise-corrected GPS time series that we derived in BH23a, considering that the GPS data are still noisy.

Figure 34: A comparison of (top) stacked tilt-meter data for Tohoku-Oki with (middle) stacked GPS data corrected for common-mode noise and (3) recorded earthquakes. Top: Fig. 3d of Hirose et al. (2024). Bottom: Fig. 15 of BH23a.

However, the data from Hirose et al. (2024) do not show any increased tilting during the 2 hours before the earthquake — there is absolutely no sign of precursory slip over this time period.

But is the tilt meter method sensitive enough? Hirose et al. calculated how small a precursory slip event would have to be to avoid detection by the tilt meters; the answer was 5.0 × 10¹⁸ Nm, or a Mw ~6.4 slow slip event. The size of the precursory slip proposed by BN23 before the Tohoko-Oki mainshock was 2.9 × 10¹⁹ Nm (~Mw 6.9) — releasing about 5.8 times more energy. Such an event is simply too large to have gone completely undetected by the tilt meters.

This appears to independently confirm that no large precursory slip happened in the two hours before the Tohoku-Oki earthquake.

What about the tilting that did happen — starting on March 9? The rising-then-flattening GPS stack is exactly what we would expect to see if the crust of Japan was stretching slightly in response to the foreshock sequence and associated aseismic slip, with the east coast of Honshu moving slightly east compared to the west coast of Honshu.

Because the tilt meter data and the GPS displacement data are independent, the apparent agreement about the timing and shape of the crustal stretching suggests that they are measuring the same crustal deformation. So, this does seem like a positive outcome of the BN23 method, which should be followed up on.

However, this presents another problem for the proposed 2-hour precursory slip. Because the similar stretching is well-resolved for the 48 hours before the M9 earthquake, and because neither time series — GPS or tilt meter — shows any precursory slip in the 2 hours before the earthquake, this actually might be a further observational confirmation of the lack of detectable precursory slip.

Note — July 27, 2024: As Prof. Bürgmann points out in the comments, the magnitude of tilting recorded by the instruments seems to exceed what is possible from foreshock-related creep. The tilt meter signal is dominated by a single station near the coast; following the largest foreshock, this station tilted progressively over the next day, with a total tilt ~200 times higher than what would be expected from aseismic creep due to the largest foreshock, which was modeled to reach ~50 cm by Ohta et al. (2012). Thus, while both stacks may reflect real processes associated with the foreshock sequence - starting at the same time and decaying with time - they cannot reflect the same processes. Hirose et al. suggest that the tilting of the station with the largest influence on the signal might be due to a problem with the instrument itself, triggered by the shaking of the M7.3 foreshock.

---

Our final takeaways

BN24 argue that it is likely incorrect to remove correlated noise in high-rate GPS prior to analyzing the stacked data, because of the risk of removing tectonic signals. They acknowledge that there is no clear proof of any earthquake signal in BN23 — but they presumably still think the data are suggestive enough that the paper should remain citable as evidence for universal precursory slip (it is certainly being cited that way already).

Based on our analysis, we evaluate the conclusions of BN24 as follows:

Though this result raises potential concerns on the tectonic origin of the proposed precursory signal, synthetic tests indicate that the common-mode filtering procedure may inadvertently remove an existing signal. (BN24)

We disagree. Our analysis demonstrates that only a small portion of the existing signal (<10% for most earthquakes) is removed. The vast majority of earthquake-like signals will be clearly retained upon removal of the far-field common mode. Thus, the obliteration of the final 2-hour spike by noise correction directly invalidates the conclusions of BN23.

Moreover, the collective outcomes of a series of tests we conducted consistently indicate that the signal points to the time, location and slip direction of the impending earthquakes with a statistical significance making very unlikely that the signal solely arises from common-mode noise. (BN24)

As discussed above, these tests are performed on the noisy data. Above, we show how some of these tests, interpreted by BN24 as evidence of a cryptic earthquake signal, can clearly be explained as arising from the common mode noise. Statistical tests chosen to emphasize the uniqueness of the signal in BN23 do not perform well against new data presented in BN24 — and ultimately only speak to the correlated GPS noise anyway. Perhaps more tests could be thought up, but unless they can somehow discriminate between the known GPS noise and real signals, they are unlikely to be any more compelling.

The alternative explanation of co-seismic contamination also appears unlikely given that the signal does not appear to be correlated with the co-seismic offsets. (BN24)

We agree: if such contamination exists, and there is no reason to think it does, it seems to fall into the correlated noise — i.e., it must come from aspects of the GPS modeling that affect entire networks, rather than individual stations. Thus, such contamination (again, if it exists) is easily remedied by common-mode noise correction.

Overall, it is difficult to definitely conclude on the origin of the signal. Nevertheless, the interpretation of the signal as indicative of precursory slip acceleration (Bletery and Nocquet, 2023) remains entirely plausible. (BN24)

We disagree. We do not see a plausible way that significant precursory slip signals could be removed by any reasonable noise correction.

References:

Bletery, Q. and Nocquet, J.M., 2024. Do large earthquakes start with a precursory phase of slow slip? Preprint at EarthArXiv, https://doi.org/10.31223/X5RT3N

Bletery, Q. and Nocquet, J.M., 2023. The precursory phase of large earthquakes. Science, 381(6655), pp.297-301. https://doi.org/10.1126/science.adg2565

Bradley, K., Hubbard, J., 2023a. Earthquake precursors? Not so fast. Earthquake Insights, https://doi.org/10.62481/310cc439

Bradley, K., Hubbard, J., 2023b. Update on apparent GPS detection of earthquake precursors. Earthquake Insights, https://doi.org/10.62481/479c2ea4

Hirose, H., 2011. Tilt records prior to the 2011 off the Pacific coast of Tohoku Earthquake. Earth, planets and space, 63, pp.655-658. https://doi.org/10.5047/eps.2011.05.009

Hirose, H., Kato, A. and Kimura, T., 2024. Did short‐term preseismic crustal deformation precede the 2011 great Tohoku‐oki earthquake? An examination of stacked tilt records. Geophysical Research Letters, 51(12), p.e2024GL109384. https://doi.org/10.1029/2024GL109384

Ohta, Y., Hino, R., Inazu, D., Ohzono, M., Ito, Y., Mishina, M., Iinuma, T., Nakajima, J., Osada, Y., Suzuki, K. and Fujimoto, H., 2012. Geodetic constraints on afterslip characteristics following the March 9, 2011, Sanriku‐oki earthquake, Japan. Geophysical Research Letters, 39(16). https://doi.org/10.1029/2012GL052430

Code:

Supporting code can be found at GitHub: https://github.com/kyleedwardbradley/BN24