The great tidal earthquake hypothesis test, part I

How might tides influence earthquakes?

Citation: Bradley, K., Hubbard, J., 2024. The great tidal earthquake hypothesis test, part I. Earthquake Insights, https://doi.org/10.62481/9ab803be

This is the first in a series of posts about whether earthquakes are influenced by tidal forces - and whether such influence might be able to tell us about upcoming large earthquakes.

In this first post, we explain the theory and methods behind a number of research papers that tackle this problem. In later posts, we will summarize the results of those papers. Then, we will replicate the methods of those papers, and test them using data from earthquakes that occurred after their publication.

Introduction

Last October, we wrote about a paper by Eric Beaucé and others that claimed that the tidal sensitivity of earthquakes increased during the years leading up to the 2019 M7.1 Ridgecrest earthquake in California. We did not find the paper convincing. But, this process got us thinking: what is the evidence for earthquakes being related to tides, and should we believe that this kind of behavior might act as a warning signal of upcoming large events?

Well, we went down a rabbit hole that we are only now starting to climb back out of. This series of post is our effort to lead you down the same rabbit hole - hopefully a less taxing trip with a guide or two - and then back out again, emerging with a fairly clear sense of what is, and is not, actually well established.

Our goal is to help anyone with an interest understand the real issues involved in this subject, so we will try to be as faithful to the science as possible while also keeping the content as accessible as we can. While the tides have long featured in crackpot earthquake predictions, this series of posts will focus on the professional scientific literature that is being commonly cited today.

“Alice started to her feet, for it flashed across her mind that she had never before seen a rabbit with either a waistcoat-pocket, or a watch to take out of it, and burning with curiosity, she ran across the field after it.” (Illustration by Sir John Tenniel for Carroll's Alice in Wonderland.)

It turns out that earthquake scientists have been trying to answer this question for over a century - and coming up with answers that vary widely, in some cases producing contradictory results. In fact, one author (Dr. T. C. Heaton, a professor of geophysics at Caltech) even wrote a paper in 1975 titled "Tridal Triggering of Earthquakes" stating that he had definitively found evidence of earthquakes being tidally controlled - only, seven years later, to apologetically write a second paper with the same name explaining that when he tried his method with new data, it fell flat. In this second paper, he wrote:

I believe that it was incorrect to apply [this analysis] to a case where the test for significance was conducted after a pattern in the data was recognized. […] This problem seems to be very common in tidal triggering studies as well as in earthquake prediction studies. We see a pattern and then ask what the probability is that this pattern would arise in a random group of numbers. It has become painfully clear that we are far better at “predicting” earthquakes after their occurrence than before.

Why is this subject so persistent over time? It is because the tides are one of the few forces that we truly know must act on faults, and for which we can actually make clear statements about stress magnitudes, directions, etc. Almost everything else about actual stresses on faults remains an observational mystery. Thus, we are compelled to search for any trace of a relationship. Added to this are tremendous but subtle cultural expectations that the Earth’s fate is governed by other celestial bodies.

The elastic deformation of the Earth (the solid earth tide) and the movement of the oceans (the ocean tide) certainly cause stresses that act within the Earth, and have the potential to affect faults. In fact, these are among the most predictable forces we could envision acting within the Earth. The fact that they are so predictable means that they can be used to some extent as an experiment -we can try to use the reaction of faults to tidal forces as a way to estimate physical properties of Earth’s interior that are almost impossible to discover any other way.

Many authors have taken up the challenge of identifying a tidal influence on earthquake nucleation, to varying results. The diversity of these studies is actually pretty astonishing, because there are so many factors at play.

We can study potential tidal triggering globally or in a particular region; for one or another type of fault; for earthquakes at sea vs. on land; for shallow or deep earthquakes; for a given range of magnitudes; for events before or after a large earthquake; for lunar, solar, or combined tides, each with many harmonic constituents; for solid earth or ocean tides; with one or another type of stress; for the magnitude, phase, or rate change of each of those stresses; for different assumed values of fault friction; for all time or just one particular window; for fast ruptures or slow slip events; using one type of statistical test or another.

That’s a lot of knobs on the tidal triggering machine! The crux of the issue is that we can’t avoid turning those knobs - we have to subset the data, driving forces, and possible responses in order to study anything.

How many knobs is too many? Why does making AI images of ambiguously happy scientists make us feel so sad?

It should be clear why this subject has been a statistical minefield since its inception. Certainly, no universal truth has emerged. Emter (1997) was somewhat flummoxed by the proliferation of at least one hundred tidal triggering studies over the previous century. A quarter century later, that number must be at 25 papers higher, right?

Let’s do a quick search on Google Scholar:

Well, that’s more results than we care to scroll through. It is likely now impossible to critically read the full literature (luckily, completely reading the literature has never been a strong requirement for doing science in any field…).

Furthermore, although the vast majority of papers that we have personally read seem to showcase one or two positive correlations, what is often ignored are the implied negative correlations with the other subsets of data that were investigated. Instead, proposed positive correlations simply accumulate in the literature while negative results are swept under the rug.

We decided to tackle this problem in pieces. In this first post, we will describe in simple terms the basic concepts - and problems - that underpin many, but certainly not all, tidal triggering studies. In the second post, we will briefly review selected papers that in our opinion stand out from the rest of the field, in terms of impact. In the third post, we will replicate some global studies of tidal triggering of large earthquakes, and test whether they hold up when we include 20+ years of new data. Then, we will examine studies about possible precursory tidal triggering - tidal earthquakes that are supposed to warn us of upcoming giant ruptures.

That should be enough to start with. It is likely that we will never actually get out of the rabbit hole, and that this will become an ongoing series as we learn more, or as more papers are published. We also look forward to getting feedback along the way, because, as usual, we are not actually subject matter experts in tidal triggering.

Illustration and text by Lewis Carroll for Alice’s Adventures Under Ground, an early manuscript of Alice in Wonderland.

To start that process, we have to begin at the beginning. Earthquakes start on faults, so we will follow their example.

Stress and faults

Before her was another long passage, and the White Rabbit was still in sight, hurrying down it. There was not a moment to be lost: away went Alice like the wind.

To understand why changing stresses can affect earthquakes, we need to think about why faults actually slip. The following discussion is simplified from a deep literature on rock and fault physics. If you are already fluent in the lingo of fault physics, feel free to read ahead.

First, close your eyes and imagine a fault inside Earth’s crust. Don’t be shy - our students (once upon a time, when we were teaching) often adopted this pose while carefully considering our lectures.

A fault is basically a closed crack surrounded by a volume of rock, which has been placed under extreme pressure. Most of the pressure is due to the weight of the overlying rock - a tremendous weight that compresses atoms and molecules together, acting equally in all directions. Because this pressure is the same in all directions, it can’t make the fault slip - every driving force is matched by an equally strong resistive force.

Now that you have an imaginary fault to work with, open your eyes and continue reading.

Faults also experience a separate, uneven pressure, which is applied by external forces. These forces are partially tectonic, ultimately arising from plate motions, and partially non-tectonic, due to other effects like Earth tides. These forces are not equally opposed, and so they can cause the fault to slip, under the right conditions.

Stress is stored energy that develops within an object, as that objects resists deformation due to applied forces. It is distributed throughout the atomic bonds and inter-atomic interactions within the object. Because planar faults don’t occupy the full rock volume, they only really care about two components of this stress - the normal stress (abbreviated as the Greek letter sigma, σ), which is perpendicular to the fault crack and causes the fault to open up or close shut, and the shear stress (Greek letter tau, τ), which tries to make the rocks on either side of the fault slip sideways.

Although these normal and shear forces are always acting on the fault, the fault usually doesn’t slip because of its frictional resistance. All along the fault surface, there are small points of contact between the two sides of the crack, making the surface rough. Even two very finely polished pieces of glass, when lightly pressed together, only actually touch at a few asperities. The size of this contact area, and the strength of the asperities, is the name of the game for fault slip.

What happens when a stable (stuck) fault experiences a Δσ - a change in the normal stress? (The symbol Δ is typically used to represent a change, for the simple reason that the Greek word for difference, diaphorá, starts with the letter delta.)

Figure 1 below shows two options.

If σ decreases (Δσ is negative), the fault will be more clamped together. The asperities will grow in size, and some new ones will form, essentially locking the fault together and making it less likely to slip. At tremendous clamping stress, the crack might actually completely seal at the atomic level.

In contrast, if σ increases (Δσ is positive), the fault will become less clamped together. The asperities will shrink, and some of them may even disappear, releasing what hold they had. This will make it much easier for the fault to slip.

Figure 1: Diagram illustrating how changes in normal stress (Δσ) can make a fault more or less likely to slip, if shear stress is held constant.

Changes to the shear stress, Δτ, can also make the fault more or less likely to slip. An increase in τ (Δτ is positive) is an increase in the sideways push, making it easier for the fault to overcome the frictional resistance by smearing out or breaking the asperities (Figure 2). A decrease in shear stress simply reduces the pushing force.

Figure 2: Diagram illustrating how changes in shear stress Δτ can make a fault more likely to slip. An increase in Δτ means the two sides of the fault are being pushed more strongly past each other, making slip easier.

We can now think more clearly about the effect of tides on a fault. The cartoon below (Figure 3) shows our imaginary fault plane riding out a tidal cycle - one cycle out of billions that have happened over geological time. The solid Earth tide is shown by the warped brown line - the surface of the solid Earth moves up and down and a bit sideways, but mostly stays in place; the interior of the Earth also moves. The liquid ocean tide is not perfectly aligned with the solid tide, because the ocean is free to slosh around. The fault experiences three effects: a change in the normal stress (Δσ), a change in the shear stress (Δτ), and a change in volume (ΔV).

(One tricky point is that we shouldn’t imagine the Moon and Sun as being overhead, generally. At high latitudes, tidal forces are almost parallel to Earth’s surface, pulling sideways instead of up. But we are mid-to-low-latitude creatures on average, so the diagram below makes more sense to us.)

(Another tricky point is that the tidal shear stress change on the fault usually doesn’t line up perfectly with its slip direction. However, tidal earthquake studies tend to look only at the component of shear stress that does line up with slip, because that is what should contribute to a rupture happening.)

Figure 3: A diagram illustrating how tides influence earthquakes.

As discussed above, there is a trade-off between normal and shear stresses: if shear stress increases but the normal stress decreases more (clamping the fault), then slip won’t happen - or vice versa. We have to look at a third parameter, called the Coulomb Failure Function (ΔCFF), which combines the two stresses.

Note: Coulomb’s (and before him, Amontons’) studies of friction produced one of the most successful empirical theories of all time, establishing a field now known as tribology. Thus, we propose that the CFF should be renamed the C-AESSF: the Coulomb-Amontons Extreme Scientific Success Function. We are not sure to which committee this suggestion should be submitted; perhaps we should consult a local tribologist.

Studies of faults in the laboratory have demonstrated that the amount of shear stress (sideways push) needed to make a fault slip depends on both the normal stress (σ) and the friction, typically represented as the Greek letter μ (mu).

That is what the Coulomb Failure Function (ΔCFF, although we hear that in high society it is increasingly being called ΔC-AESSF) measures.

In technical symbols,

\(ΔCFF = Δτ + μΔσ\)

A positive ΔCFF can be associated with either positive or negative changes to normal stress, and either positive or negative changes to shear stress! So, looking at the normal or shear stress alone should be a pretty poor measure of whether the fault is more or less likely to slip.

However, ΔCFF comes with a complication. Since we don’t actually know the friction on the fault, we have to allow a range of possibilities. Studies of faults suggest that friction is probably somewhere between 0.1 and 0.9, depending on the fault. So, studies of tidal forcing tend to include a few values within this range. This isn’t a perfect solution, since different faults likely have different values of friction, but it should be better than looking at either shear or normal stress alone. In the our posts, the ΔCFF is identified with the value of friction - for instance, a ΔCFF calculated with a friction of 0.1 is ΔCFF(0.1), while a ΔCFF calculated with a friction of 0.7 is ΔCFF(0.7).

There is one additional parameter that might influence fault slip: the change in volume (Figure 4). Unlike the normal stress, shear stress, and ΔCFF, ΔV is independent of the fault: it tells us something about the whole rock - it is either shrinking (getting more dense) or expanding (getting less dense). (Obviously, this change in volume is very, very small.)

Figure 4: Stress changes can also cause the rock to expand or contract. Here, σU, σN, and σE represent the stresses in the up, north, and east directions.

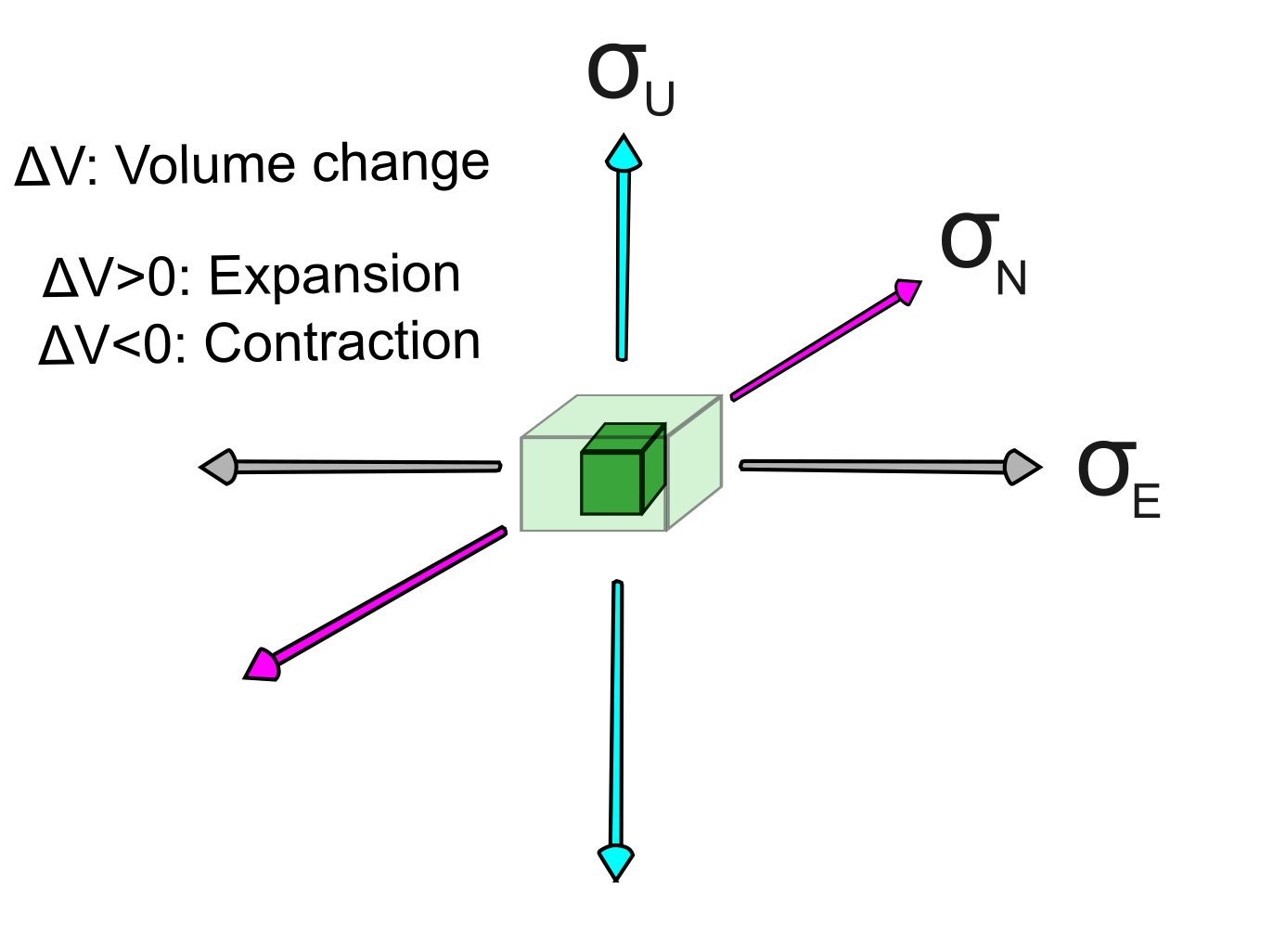
Why might ΔV matter? Models of faults have shown that small changes in volume can influence earthquake nucleation, with earthquakes more likely to start in rock volumes experiencing dilatancy, which is basically a fancy word for expansion, or an increase in ΔV (Figure 5). Dilatancy can arise from physical effects on the fault itself, like when strong asperities try to ride past each other, pushing the fault apart.

Figure 5: Part of Figure 8b of Caniven et al., 2021

One could reasonably hypothesize that an externally imposed dilatancy, caused by tidal volume changes, could also have a similar effect in promoting rupture. Thus, we have to add ΔV to the list of things to compare to earthquakes, in addition to Δτ, Δσ, and ΔCFF.

Finally, it is important to note that when an earthquake occurs, we do not actually know the orientation of the fault plane. While this orientation is not relevant for measuring ΔV, it is necessary in order to estimate Δτ, Δσ, and ΔCFF. Fortunately, for earthquakes that are large enough, seismologists can calculate a focal mechanism. A focal mechanism is represented by a weird “beachball” - a sphere cut by two perpendicular planes (Figure 6). One of those two planes represents the fault orientation; the other tells us about the direction of slip in the earthquake. There is no way to tell from a focal mechanism which of the two planes actually slipped.

It turns out that the magnitude of the shear stress (Δτ) is the same for both of these planes. Δσ and ΔCFF, however, depend on the specific fault plane. For this reason, some tidal earthquake researchers choose to look at only Δτ; others select one plane over the other for geological reasons (for instance, the low-angle plane in shallow subduction zones, or the plane that aligns with a nearby large strike-slip fault).

Figure 6: A focal mechanism with two possible fault planes and direction of slip. Each image shows half of the focal mechanism, assuming that one or the other nodal plane is the fault.

Estimating tidal stress changes

‘Up above the world you fly,
Like a tea-tray in the sky.’

For a fault at a given latitude, longitude, and depth, we can calculate how tidal forces change the stresses in the rock around the fault, and then estimate the stresses acting on the fault plane itself.

This calculation is a fairly high technology endeavor, because we need to account for the orbital parameters of the Sun, Moon, and Earth, the material structure of the Earth, and the motion of the ocean. Luckily, several open source codes developed with great care over decades are available. Across this series of posts, we will use the recently updated TidalStrain.2 code of Hirose et al. (2022), so that we can compare results directly to some published papers.

In Figure 7, we plot the changing stresses on a hypothetical fault. For each curve, the period when the value is positive (shaded light gray) is when we should expect that change in stress to promote fault slip. When the curve is negative, it should impede fault slip (shaded darker gray).

Figure 7: Example tidal stress and volume change calculations, for about four tidal cycles (48 hours).

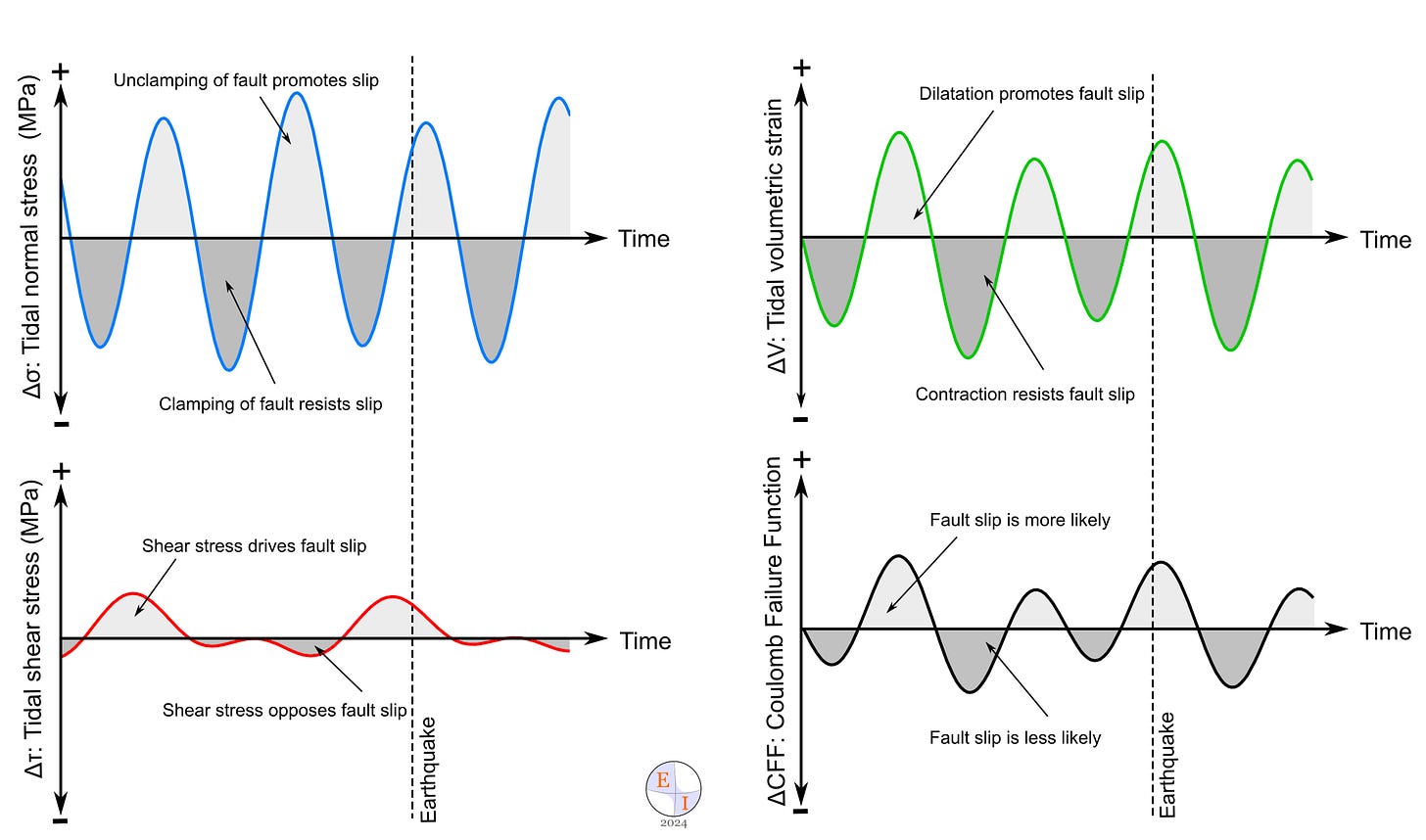
You can see that the normal stress (blue) and shear stress (red) don’t have the same phase - sometimes normal stress is positive while shear stress is negative. So should the fault slip or not? This is the problem that ΔCFF is supposed to solve - it takes into account both parameters (Figure 8). ΔCFF is a weighted sum of the two components. which means that since normal and shear stress are generally not in phase with each other, ΔCFF will have some new phase that matches neither. That new phase should represent the likelihood of slip on the fault better than either of the components alone. However, the shape of the curve depends on the assumed friction.

Figure 8: How ΔCFF is calculated using Δτ and Δσ.

Since an earthquake occurs at a specific time, we can use these calculations to find the values of Δτ, Δσ, ΔV, and ΔCFF at that specific time, for that specific earthquake. But, it turns out that most researchers don’t actually do this. Instead, they use a different number, called the tidal phase.

It’s just a phase, right?

“I’m afraid I can’t put it more clearly,” Alice replied very politely, “for I can’t understand it myself to begin with; and being so many different sizes in a day is very confusing.”

The problem with using the amplitude (i.e. value) of the stresses is that it makes some statistical comparisons difficult. This is because a fault might spend a lot of time at one stress amplitude, and very little time at another - so if you look at the frequency of earthquakes, you would naturally see many more at the first and many fewer at the second, even if the earthquakes are occurring randomly.

To solve this problem, most (but not all) studies measure the tides using their phase. The tidal phase is indirect and imperfect, but it solves the problem above, since phases are equally distributed over time, at least over long time periods. Thus, if there is a clear relationship between tidal phase and earthquake frequency, it should be telling us that tides affect earthquakes.

Calculating the tidal phase is pretty easy (Figure 9). Given an earthquake at a specific time, find the two lowest points in the tidal stress curve before and after the earthquake, and find the peak between them. From earlier to later, give these times phase values of -180°, 0°, and +180°. Then, distribute the phases equally between these points. For instance, the time halfway between -180° and 0° will have a phase of -90°, while the time halfway between 0° and +180° will have a phase of +90°. Typically, phases of -90° and +90° will fall near (but not exactly on) the x-axis (where the stress value is close to zero). However, when tides are more irregular, it is possible for a whole cycle of tidal phases (from -180° to +180°) to occur below or above the x-axis.

Figure 9: Illustration of how phase is defined across one tidal cycle (-180° to 180°) surrounding an earthquake time. While phase is a continuous value, we color it by division into 30° blocks, which are evenly spaced in time between each pair of values of -180°, 0°, +180°, and 0°. The earthquake shown here has a phase of +45°.

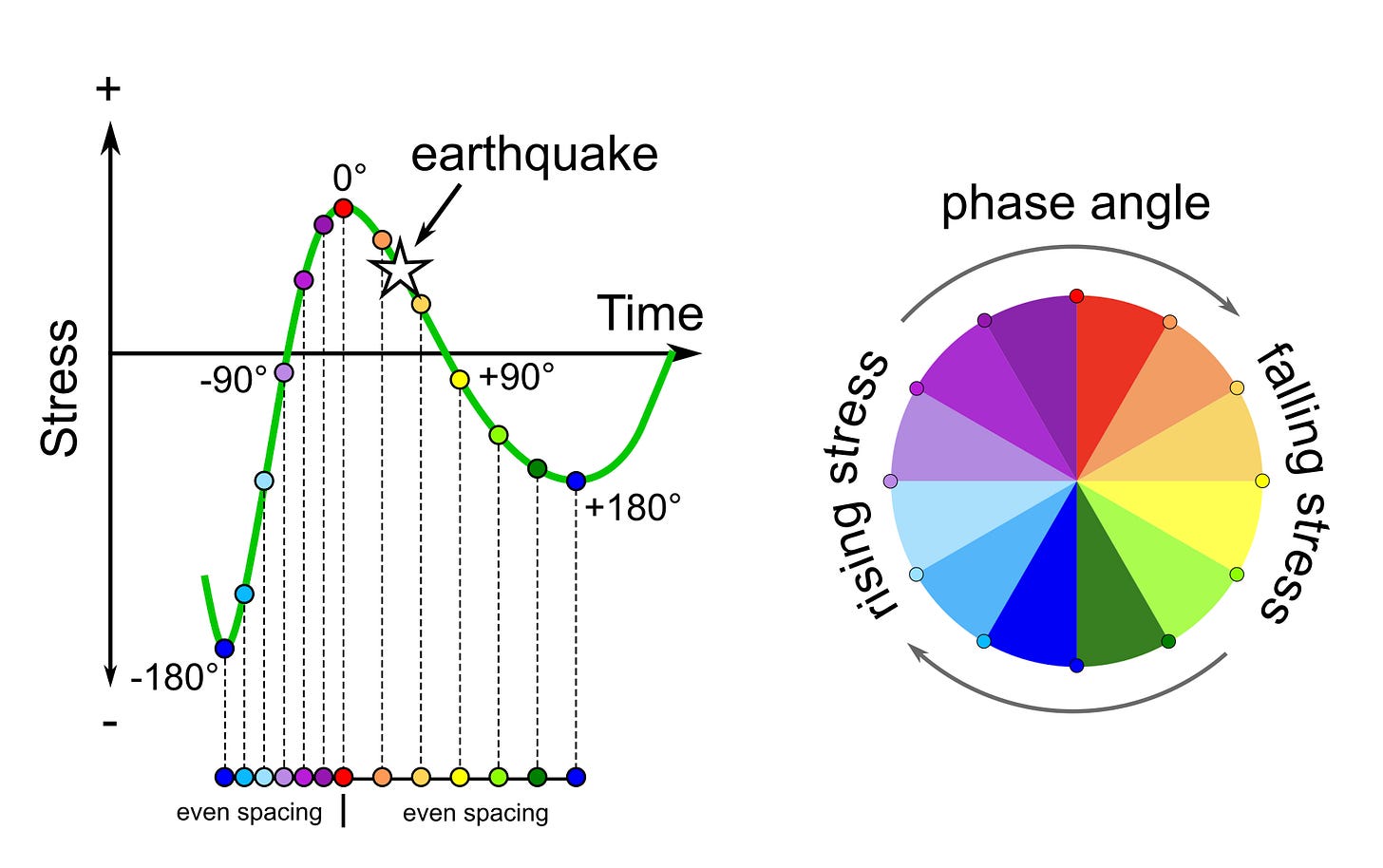
So, what does tidal phase tell us? Values close to 0° indicate that the stress is at its highest value in that particular tidal cycle. For shear stress, that means the fault is experiencing the strongest sideways push; for normal stress, the most unclamping; for CFF, the fault is most likely to slide; for volume, the rock has expanded the most. These values do not tell us about the magnitude of the stress change - simply about how that moment compares to other moments during that particular cycle.

Figure 10: Tidally caused Δσ (top left), Δτ (bottom left), ΔV (top right), and ΔCFF (bottom right) for a fault that experienced an earthquake (vertical dashed line). Colored circles show phase increments of 30°.

We can use the phase to understand whether stress is increasing or decreasing: phase values from -180° to 0° occur when the stress is rising on the fault, while values from 0° to +180° occur when the stress is falling on the fault (Figure 10).

Studies of tidal forcing generally (but not always) compare these phases of the various tidal stresses that existed at the times and locations of earthquakes, and try to determine if those phases are random, or if earthquakes tend to occur more often at specific phases.

To understand how the test is usually done, we need to go on a walk.

Schuster’s test, and other statistical approaches to assess correlation

When you think you are using a reliable statistical method, but discover that you are actually holding a flamingo. (Illustration by Sir John Tenniel for Carroll's Alice in Wonderland.)

In 1897, Fellow of the Royal Society (and originator of the concept of antimatter) Sir Franz Arthur Friedrich Schuster proposed a simple statistical test that could be applied to the problem of tidally triggered earthquakes. This test was created in response to dubious claims that earthquakes were in fact caused by tides. It is important to remember that in 1897, it was still not known that earthquakes arose from rupture of faults deep within the Earth. At that point, there had been only a few observations of surface rupture, including after the 1891 Nōbi earthquake in Japan, and surface ruptures - like most other effects that we can see directly - were thought of as a product of earthquake shaking rather than its cause. Theories of earthquake generation by underground explosions, magma intrusions, or shifts caused by the lunar tides, were common at that time.

Prof. Schuster thought that the tidal origin claims basically amounted to confirmation bias, because published calculations had no statistical baseline for comparison. After all, if you don’t know what a random signal would look like, how can you tell whether the behaviour you are seeing is random? So, Schuster invented a test, now called the Schuster Test, intended to calculate how improbable a sequence of earthquakes was.

As applied to earthquake tides, the test can be paraphrased like this:

Place a point at the origin on an X-Y plane. For each earthquake that occurs, determine the phase angle of the relevant tidal stress (Schuster used the timing of the meridian passage of the moon, not tidal stresses as discussed above), and move one step in the compass direction that is equivalent to that phase angle (Figure 11). For instance, a phase angle of 0° equals a step to the north. After N equal length steps (associated with N earthquakes, each with its own tidal phase), measure the distance D between the end point and the origin.

Schuster determined that the probability of a random walk with N steps reaching a distance D from the origin can be calculated using the simple formula:

\(p = e^{-D^2/N}\)

That is, for random walks, 10% of them should have p-value below 0.1, 50% should have p-value below 0.5, etc. This value allows us to say with greater certainty whether a collection of steps (phases) has some preferred direction. In statistics-speak, we can reject the null hypothesis that the tidal phases are random with probability (1-p)%.

Figure 11 illustrates three different “Schuster walks”, which all start at the origin and take seven steps, ending in different locations:

Figure 11: Three different possible Schuster walks of seven steps each (N=7). At the end of each walk, p, the percentage of random walks that reach a distance D can be calculated using the equation above.

If the path returns to the origin (the pink walk), then D = 0. This walk simulates the path of someone who has had a few too many pints discussing earthquake statistics with Prof. Schuster down at the local pub. We could never assert that the walker had a given direction in mind (1-p = 0%).

If instead there is a slight preference for one range of angles (the red walk), then the walk will drift slowly in that direction, ending farther from the origin. Perhaps, having recovered a bit, Prof. Shuster’s pub companion is now stumbling home. In this case, only 21% of random walks would go this far. The preferred phase falls between -20° and -30°, north-northwest.

If only one phase angle occurs, then the walk will be a straight line headed for the horizon (the blue walk). This is reliable Prof. Shuster, who drank only water and needs to reach the comfort of his own privy at home. Only 0.09% of random walkers would make it this far (p=99.91% that Prof. Shuster is not randomly walking).

Using this method, we should be able to detect a preference for tidal phase by looking at a collection of earthquakes and calculating the p-value.

Now - it is important to note that the Schuster Test does not say that a low p value (a high probability of not being random) is consistent with fault stresses. That only happens if p is low, and the preferred phase is close to 0°. If the phase is lower than -90° or higher than 90°, then the stresses should actually inhibit earthquake nucleation. As we will see in later posts, this point is sometimes ignored.

We are almost done with the background theory - but important matters remain.

A complication with earthquake locations

Alice had no idea what Latitude was, or Longitude either, but thought they were nice grand words to say.

Where does an earthquake occur? Although earthquakes are often represented as points on maps, they actually occur due to slip on 3D surfaces (faults). For small earthquakes, a point might be a good-enough representation. For large ones, with ruptures that span hundreds of kilometers, a point is clearly an oversimplification.

However, for the purposes of earthquake initiation, a point still carries meaning. This is because every earthquake starts at a point. The location of that point - the earthquake origin, or hypocenter - can be estimated, giving it a latitude, longitude, and depth.

The first P-wave arrivals recorded on seismograms originate from this point, because the seismic wave speeds through the Earth are faster than the rupture propagation speed along the fault.

There is another point location that is commonly reported for earthquakes: the earthquake centroid. This location is supposed to represent the “average” location of the earthquake, taking into account the rupture across the fault - it is the location and time of the average energy radiation (Figure 12). This is usually closer to the area of peak slip, which might be far away from the origin point, if the rupture was large.

Figure 12: Block model of a theoretical fault plane (pink) with a rupture patch (gray). Arrows represent the rupture path; dashed lines are contours of the rupture front as it progressed through time. Red line with teeth shows intersection of the rupture with the surface. Coastal residents should head for the hills!

Most tidal earthquake studies use earthquake catalogs (primarily the Global Centroid Moment Tensor catalog) that contain both types of information: both origin and centroid locations. This is because these earthquakes have been well-studied enough to generate focal mechanisms, which are needed to reveal the orientations of the two possible fault planes - making it possible to calculate Δτ, Δσ, and ΔCFF on an earthquake-by-earthquake basis. This shouldn’t be a problem, since the origin location is available for each earthquake.

However, when we started trying to replicate studies, we realized that a number of them use the centroid locations, rather than origins. This might not seem like a big problem, since only for really large earthquakes should the origin and centroid be very far apart.

EXCEPT:

There is an additional difference between centroid and origin locations, which arises from the different methods used to calculate the locations.

All earthquake locations are estimated using a 3D velocity model, in order to backtrack from where the earthquake was detected (a seismometer) to where it started. The speed at which the waves travel is necessary for this calculation - and it varies based on rock type, rock temperature, depth, and more.

Focal mechanisms usually require observations from distant stations, often located many thousands of kilometers away from the hypocenter. The velocity model needs to take into account the structure of the deep Earth as well as the propagation of waves trapped at the surface. In contrast, earthquake origin locations are typically inferred from nearby seismometers, which record the seismic waves soon after they are born, and before the waves have passed through much of Earth’s complex geology. Accurate location of hypocenters by a regional seismic network does not require a very complex velocity model, although a good one usually helps.

The global 3D velocity model used to calculate GCMT centroids is different from the velocity models used to identify the origin location. This velocity model difference can cause an artificial horizontal and vertical offset between origin and centroid - a location bias - that varies in size and offset direction around the world. In a focal mechanism calculation, you have to trade off uncertainties; GCMT tries to stuff the uncertainties into the location, in order to better resolve other details about the earthquake. The existence of regional biases in GCMT centroid locations is well known (e.g. Hjörleifsdóttir and Ekström, 2010).

How much does this bias matter? First, it depends on where you are on Earth, because most of Earth’s surface is covered by water where seismometers don’t really work. Then, because different types of earthquakes radiate seismic waves at different powers in different directions, it also depends on the kinds of earthquakes you are looking at. For Sumatra (Figure 13), the centroids of strike-slip and normal earthquakes are generally ~10-20 km away from their origins; for thrust events, the difference is larger - ~10-80 km. We will discuss the geology of this area in post IV of this series, in relation to tidal triggering of earthquakes in this area.

Figure 13: Earthquakes with focal mechanisms in the region around Sumatra. Earthquakes are plotted at their origin locations, and colored by how far away the centroid location is. Left plots show histograms of centroid-origin distance for three classes of faults.

Because tidal phase depends on the motion of the ocean, earthquakes occurring in coastal areas can have significantly different phase at the origin and centroid location. In our following posts, we will show how erroneous use of the centroid location significantly impacts some published results. For now, let’s just keep in mind that we should always be thinking about the origin location when we are talking about earthquake nucleation.

Beware of aftershocks and swarms

“What a funny watch!” she remarked. “It tells the day of the month, and doesn’t tell what o’clock it is!”

“Why should it?” muttered the Hatter. “Does your watch tell you what year it is?”

“Of course not,” Alice replied very readily: “but that’s because it stays the same year for such a long time together.”

What triggers an earthquake? For many events, the triggering effect is well-known: earthquakes trigger other earthquakes. Every earthquake triggers a large number of other events, with a rate that decays with time; this is known as Omori’s Law. The cause of this is stress changes associated with slip on nearby faults, which are generally much greater than any stress changes caused by tidal effects.

Swarms are another example of earthquakes that are related to each other: events that occur closely spaced together over some period of time - much longer than one or a few tidal cycles. Swarms are often thought to be associated with fluids or magma, and can involve bursts of seismicity. For instance, Iceland has seen a large number of earthquakes in recent months, associated with dike intrusions; these events are considered to be associated with magma injection and eruption, not tides.

When an earthquake has a known trigger - the stress changes induced by another earthquake, or magma movement - it should not be interpreted as triggered by tiny tidal stresses using the framework we have described above.

So, what’s the problem? Immediately after a large earthquake, aftershocks occur close together in time, slowly becoming more spaced out. That means that there will be more aftershocks in the first three hours than in the next three hours, and so on. In other words, more earthquakes will occur during the tidal phase that existed during those first three hours. That correlation with tidal phase could easily be interpreted as tidal influence, but it is not. The same effect can be observed for earthquake swarms - and since these events are usually linked to some persistent physical driving mechanism, we should not interpret them as tidal.

If we look at a recent earthquake (the January 1, 2024 Noto earthquake in Japan), we can see that M3+ earthquakes are concentrated during rising ocean tides, because that’s when the main shock struck (Figure 14). A histogram shows that the rate of earthquakes in the initial aftershock sequences was highest between 8 AM and 9 AM (UTC time) - about an hour after the 07:10:22 main shock, when small events started to become detectable above the noise caused by the mainshock. This is a casual analysis, but is intended to show the problem posed by temporally clustered earthquakes.

Figure 14: Left: colored bars: histogram of earthquakes in each hour from December 31, 2023 through January 3, 2024. Black line: ocean height due to tides during the same period. Right: Histogram of earthquakes for the same time period, classified by hour of day. Earthquake data are from JMA. Tide level data is from worldtides.info.

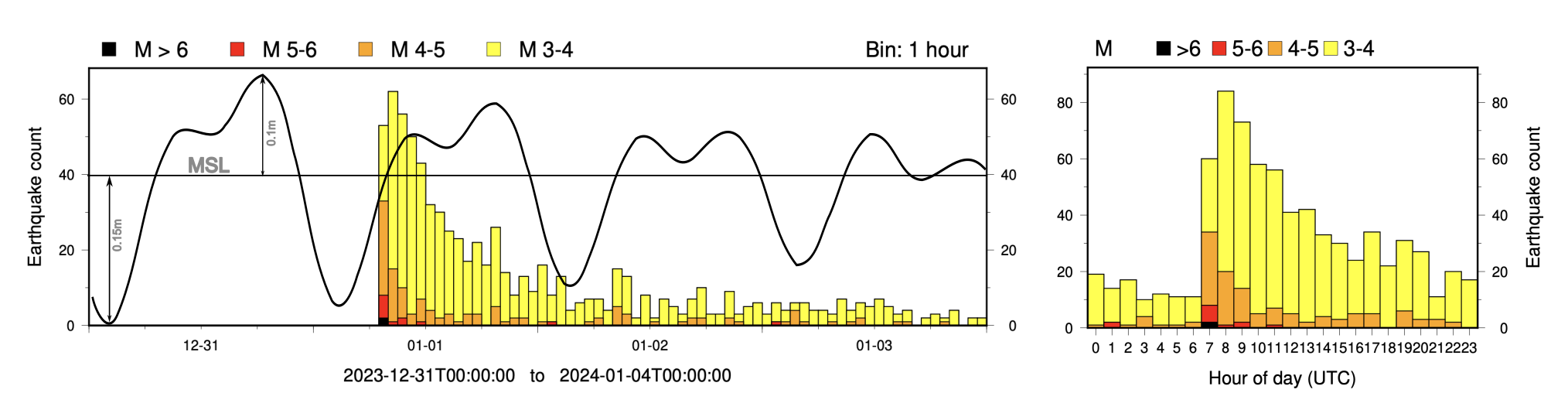
What’s the solution? Aftershocks actually cause statistical problems for a lot of earthquake studies - and have been addressed through a process called declustering: identifying and removing excess earthquakes thought to represent aftershocks of other events. Declustering is difficult and there is no one way to do it, but a number of algorithms have been developed for this purpose. However, declustering will not remove swarm seismicity, because the triggering effect is not the stress interactions of the small earthquakes, but some other physical process.

For the purposes of tidal studies, we can be a bit more casual: if we simply throw out any earthquake within a certain distance and time of a previous earthquake, we can remove any artificial tidal correlation caused by both aftershocks and swarms. We might throw out a few earthquakes unnecessarily, but that should not remove any tidal signal, should one exist. Tidal studies do not argue that earthquakes are triggered within a single 12-24 hour tidal cycle, but that faults are equally susceptible to every tidal cycle, with a tendency to rupture during a specific tidal phase. If you found many earthquakes during a single 6-hour period, you would not interpret that as tidal, even though the seismicity would be correlated with a specific tidal phase.

For studies that use only focal mechanisms (like the GCMT catalog), the effect of aftershocks is likely small. First, focal mechanisms are only available for earthquakes above a certain magnitude, and there are not that many of them to begin with. Second, a large earthquake creates waves that continue to reverberate for a long time period, making it difficult to calculate focal mechanisms for smaller events during the time immediately following the mainshock. Thus, the GCMT catalog is naturally “declustered” to some degree. Some aftershocks may remain, and swarms will continue to affect these catalogs, since there is no mainshock to cause noise.

For more complete catalogs of earthquakes (without focal mechanisms) however, both aftershocks and swarms likely have a large influence. This effect will be especially strong for small earthquakes, and in regions where aftershocks are well detected - i.e., on land, in areas with good seismometer networks.

This series represents our attempt to understand the issues at hand. In the following posts, we will be characterizing other people’s work, sometimes a bit negatively, based on our own evaluations of the science. Those criticisms should be tempered by the understanding that tidal earthquake science is tricky, and it is always harder to create something than it is to knock it down. We hope that people view our comments as the beginning of a thought process rather than an authoritative opinion. Hopefully, we can lay out our thoughts clearly enough that any flaws in our own understanding are obvious. If you have anything to add to the discussion so far, please leave a comment.

You have now entered the rabbit hole. Our next post will take us deeper - exploring the results in the peer-reviewed, published literature. Beware of statistical traps, and keep an eye out for the Cheshire Cat!

Illustration by Sir John Tenniel for Carroll's Alice in Wonderland.

“There’s more evidence to come yet, please your Majesty,” said the White Rabbit, jumping up in a great hurry; “this paper has just been picked up.”

“What’s in it?” said the Queen.

“I haven’t opened it yet,” said the White Rabbit.

References:

Beaucé, E., Poli, P., Waldhauser, F., Holtzman, B. and Scholz, C., 2023. Enhanced tidal sensitivity of seismicity before the 2019 magnitude 7.1 Ridgecrest, California earthquake. Geophysical Research Letters, 50(14), p.e2023GL104375. https://doi.org/10.1029/2023GL104375

Bradley, K., Hubbard, J., 2023. Do Earth tides warn of impending large earthquakes? Earthquake Insights, https://doi.org/10.62481/695e5945

Caniven, Y., Morgan, J.K. and Blank, D.G., 2021. The role of along‐fault dilatancy in fault slip behavior. Journal of Geophysical Research: Solid Earth, 126(11), p.e2021JB022310. https://doi.org/10.1029/2021JB022310

Dziewonski, A. M., Chou, T.-A., and Woodhouse, J. H., 1981, Determination of earthquake source parameters from waveform data for studies of global and regional seismicity, J. Geophys. Res., 86, 2825-2852, https://doi.org/10.1029/JB086iB04p02825

Ekström, G., Nettles, M., and Dziewonski, A. M., 2012. The global CMT project 2004-2010: Centroid-moment tensors for 13,017 earthquakes, Phys. Earth Planet. Inter., 200-201, 1-9. https://doi.org/10.1016/j.pepi.2012.04.002

Emter, D., 1997. Tidal triggering of earthquakes and volcanic events. Tidal phenomena, pp.293-309. https://doi.org/10.1007/BFb0011453

Heaton, T.H., 1975. Tidal triggering of earthquakes. Geophysical Journal International, 43(2), pp.307-326. https://doi.org/10.1111/j.1365-246X.1975.tb00637.x

Heaton, T.H., 1982. Tidal triggering of earthquakes. Bulletin of the Seismological Society of America, 72(6A), pp.2181-2200. https://doi.org/10.1785/BSSA07206A2181

Hirose, F., Maeda, K. and Kamigaichi, O., 2022. Efficiency of earthquake forecast models based on earth tidal correlation with background seismicity along the Tonga–Kermadec trench. Earth, Planets and Space, 74(1), pp.1-11. https://doi.org/10.1186/s40623-021-01564-4

Hjörleifsdóttir, V. and Ekström, G., 2010. Effects of three-dimensional Earth structure on CMT earthquake parameters. Physics of the Earth and Planetary Interiors, 179(3-4), pp.178-190. https://doi.org/10.1016/j.pepi.2009.11.003

Hubbard, J. and Bradley, K., 2024. M7.5 earthquake strikes western Japan, triggers tsunami. Earthquake Insights, https://doi.org/10.62481/e8bf9b2e

Hubbard, J. and Bradley, K., 2023. Volcanic earthquakes in Iceland. Earthquake Insights, https://doi.org/10.62481/417cdab2

Schuster, A., 1897. On lunar and solar periodicities of earthquakes. Proceedings of the Royal Society of London, 61(369-377), pp.455-465. https://doi.org/10.1098/rspl.1897.0060